セレクタを示せ
1 君の輪郭に触れたい
「お願い♪タッチ♪タッチ♪ここにタッチ♪あなたから♪」このフレーズは人気アニメ「タッチ」の主題曲のものだ。これを女子が歌うと、「いいのか?本当にいいのか?」と、
私は心の中で思ってしまう(^^!) まぁ女子に触れたい願望は置いといて、今回は画像の輪郭抽出の話である。当文書が対象にするゲームでは、施設の建設を行う事が出来る。
建設した数ある施設の中からゲーム操作の対象を選ぶ。どの施設が選ばれているのかを、視覚的に表現しプレイヤーに伝える必要がある。
 選択するには任意の施設をクリックする。選択された施設の輪郭を赤線表示する事で、視覚的な表現にしようと言うわけだ。この赤線表示の輪郭をセレクタと呼ぶ事にする。
選択するには任意の施設をクリックする。選択された施設の輪郭を赤線表示する事で、視覚的な表現にしようと言うわけだ。この赤線表示の輪郭をセレクタと呼ぶ事にする。
例の如く、輪郭抽出や輪郭処理のワードでネットを検索したのだが、学術的な記述が多く、私の頭で理解可能なページはあまりない。しかしわかりやすい解説のページがあったので 参考にしたページを上げておく。このページによると
二値化とは男と女、善と悪、50以上と50未満などの真偽判定により区別可能な値に仕立てる事だ。画像処理においては白と黒を用いる事が多い。ここで扱う施設の画像では、 黒の完全な透明と以外で判別する。施設画像はそのように作成済みであるから、区別可能な値に仕立てる事は不要となる。 次に連結部分とはなにか?う~ん良くわからん(^^!) 画像の中のある画素について着目している時に、着目点から4近傍(上下左右)を判定するか、8近傍(4近傍+4つの斜め方向)を 判定するかで、4近傍を4連結、8近傍を8連結と、言うらしい。まぁ厳密な定義の意味は無視しておく。当該処理では8近傍を採用する。高度な画像処理では、 状況に応じて4近傍と8近傍を切り替えながら処理するみたいだが、私には無理なので8近傍一点で攻める事にする。
 選択するには任意の施設をクリックする。選択された施設の輪郭を赤線表示する事で、視覚的な表現にしようと言うわけだ。この赤線表示の輪郭をセレクタと呼ぶ事にする。
選択するには任意の施設をクリックする。選択された施設の輪郭を赤線表示する事で、視覚的な表現にしようと言うわけだ。この赤線表示の輪郭をセレクタと呼ぶ事にする。例の如く、輪郭抽出や輪郭処理のワードでネットを検索したのだが、学術的な記述が多く、私の頭で理解可能なページはあまりない。しかしわかりやすい解説のページがあったので 参考にしたページを上げておく。このページによると
二値化された画像において、各連結部分の境界部分を求める事を輪郭追跡といいます。とある。
二値化とは男と女、善と悪、50以上と50未満などの真偽判定により区別可能な値に仕立てる事だ。画像処理においては白と黒を用いる事が多い。ここで扱う施設の画像では、 黒の完全な透明と以外で判別する。施設画像はそのように作成済みであるから、区別可能な値に仕立てる事は不要となる。 次に連結部分とはなにか?う~ん良くわからん(^^!) 画像の中のある画素について着目している時に、着目点から4近傍(上下左右)を判定するか、8近傍(4近傍+4つの斜め方向)を 判定するかで、4近傍を4連結、8近傍を8連結と、言うらしい。まぁ厳密な定義の意味は無視しておく。当該処理では8近傍を採用する。高度な画像処理では、 状況に応じて4近傍と8近傍を切り替えながら処理するみたいだが、私には無理なので8近傍一点で攻める事にする。
2 私を走査しなさいよ
二値化された画像に対して、どこから近傍探索を行うかを決定するために、最初の画素を見つける必要がある。一般的には画像の左上からラスタスキャンを行い最初の画素とする。
一般的とは未知の画像に対して汎用的に扱う意味である。しかし当該施設画像には既知の仕様がある。施設画像は菱形のグリッド上に配置される。よって菱形のグリッドの水平対角線の
垂直位置から最初の画素を見つければ良い。

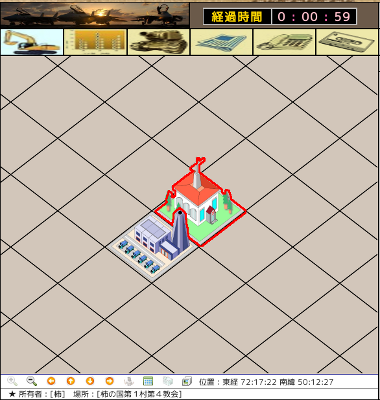 左側の図は処理する画像のイメージである。地面レイヤと施設レイヤ、それと菱形のグリッドレイヤとセレクタ描画レイヤを重ねて表示している。輪郭追跡の対象はセレクタ描画レイヤである。
走査開始点のY座標を菱形の対角線の交点とする。黒の完全透明な画素でない最も左端の座標を近傍探索の最初の画素とする。これによりラスタスキャンする行は1行のみとなる。
左側の図は処理する画像のイメージである。地面レイヤと施設レイヤ、それと菱形のグリッドレイヤとセレクタ描画レイヤを重ねて表示している。輪郭追跡の対象はセレクタ描画レイヤである。
走査開始点のY座標を菱形の対角線の交点とする。黒の完全透明な画素でない最も左端の座標を近傍探索の最初の画素とする。これによりラスタスキャンする行は1行のみとなる。
施設画像は奥行きを持つように配置する。つまり垂直位置が小さい値のものを先に表示する事で重なりが生じる。この様子を右側の図は示している。この重なりを排除した画像に対して 輪郭追跡を行う。クリックされた施設に対して重なる可能性のある施設は、左下、真下、右下の3施設になる。そのように施設画像は作成する仕様にしてあるので他の可能性は考慮しない。 施設画像の重なりを排除する処理は以下のようになる。
1) セレクタ描画レイヤに着目画像(クリックされた施設)を貼り付ける。
・globalCompositeOperation = "copy" で上書きにする。
2) 下段(左下、真下、右下)の画像を合成する。
・globalCompositeOperation = "destination-out" で描画した画像が黒の透明になるようにする。
globalCompositeOperation や drawImage はHTML5で登場した canvas タグ(実際はコンテキスト)に対するプロパティとメソッドだ。この文書の読者は、canvas タグに対する知識がある事を、 前提にしているので詳細については割愛する。雰囲気を味わってもらうために、ソースの一部を掲載しておく。これで輪郭追跡の準備が出来たので、次節では輪郭追跡の処理について記述する。

 左側の図は処理する画像のイメージである。地面レイヤと施設レイヤ、それと菱形のグリッドレイヤとセレクタ描画レイヤを重ねて表示している。輪郭追跡の対象はセレクタ描画レイヤである。
走査開始点のY座標を菱形の対角線の交点とする。黒の完全透明な画素でない最も左端の座標を近傍探索の最初の画素とする。これによりラスタスキャンする行は1行のみとなる。
左側の図は処理する画像のイメージである。地面レイヤと施設レイヤ、それと菱形のグリッドレイヤとセレクタ描画レイヤを重ねて表示している。輪郭追跡の対象はセレクタ描画レイヤである。
走査開始点のY座標を菱形の対角線の交点とする。黒の完全透明な画素でない最も左端の座標を近傍探索の最初の画素とする。これによりラスタスキャンする行は1行のみとなる。施設画像は奥行きを持つように配置する。つまり垂直位置が小さい値のものを先に表示する事で重なりが生じる。この様子を右側の図は示している。この重なりを排除した画像に対して 輪郭追跡を行う。クリックされた施設に対して重なる可能性のある施設は、左下、真下、右下の3施設になる。そのように施設画像は作成する仕様にしてあるので他の可能性は考慮しない。 施設画像の重なりを排除する処理は以下のようになる。
1) セレクタ描画レイヤに着目画像(クリックされた施設)を貼り付ける。
・globalCompositeOperation = "copy" で上書きにする。
2) 下段(左下、真下、右下)の画像を合成する。
・globalCompositeOperation = "destination-out" で描画した画像が黒の透明になるようにする。
globalCompositeOperation や drawImage はHTML5で登場した canvas タグ(実際はコンテキスト)に対するプロパティとメソッドだ。この文書の読者は、canvas タグに対する知識がある事を、 前提にしているので詳細については割愛する。雰囲気を味わってもらうために、ソースの一部を掲載しておく。これで輪郭追跡の準備が出来たので、次節では輪郭追跡の処理について記述する。
// 着目画像を貼り付け ctxRst.globalCompositeOperation = "copy"; ctxRst.drawImage(img[0], x, y, w, h); // 下段(左下、真下、右下)の画像を合成する for (var idx = 1; idx < img.length; idx++) { if (img[idx]) { // 切り取り画像のサイズと位置の設定 var dw = g_Bd.Zoom4Width; var dh = img[idx].height; var dx = (pos[idx].x - mi.MapX) - (dw / 2); var dy = (pos[idx].y - mi.MapY) + (mi.GridCY / 2) - dh; // 切り取り画像の貼り付け ctxRst.globalCompositeOperation = "destination-out"; ctxRst.drawImage(img[idx], dx, dy, dw, dh); } }
3 やさしく八近傍で攻めてね
輪郭追跡の処理アルゴリズムで参考にしたページでは、
「最後にスタート地点に戻ったら処理は終了です。」とある。輪郭追跡のループ構造としては左下枠内の記述ような感じだろう。入れ子ループの for は8近傍を見るループだ。
St はラスタスキャンで見つけた最初の画素の座標だ。px と py は検索した画素の座標を表す。di は一つ前の輪郭の向きの値を示す。for のループ変数 nv は輪郭の検索の向きの値を示す。
向きの値とは8方向を 0~7 の値にしたものだ。0:左下 1:下 2:右下 3:右 4:右上 5:上 6:左上 7:左 となる。di と nv の組み合わせの数は 8×8 = 64 通りある。
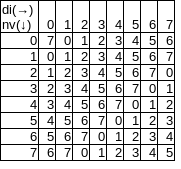 左表は di と nv の組み合わせを示している。この表をTとすると、T[nv, di] は次に判定する画素の方向を示す。T[0, 0] は7だから左の画素を見る。
T[0, 1] は0だから左下の画素を見ると言った具合だ。有効画素であった場合は、di に nv を記憶し for ループを脱出する。
左表は di と nv の組み合わせを示している。この表をTとすると、T[nv, di] は次に判定する画素の方向を示す。T[0, 0] は7だから左の画素を見る。
T[0, 1] は0だから左下の画素を見ると言った具合だ。有効画素であった場合は、di に nv を記憶し for ループを脱出する。
左表の二次元テーブルを変数にして処理したら、次の判定画素を確定する事は可能だ。しかし表を見ると直感的に何かしらの規則性があるように感じる。 つまり表を変数にしなくても計算により導き出せるのではないか?と感じる。表の要素は何かを8で割った時の余りになるような気がする。8方向は 0~7 の値をとるからだ。 (nv + di + 7) % 8 ならどうだろう?おぉズバリじゃないか。これで表の変数は不要だ。
ところで参考にしたページによれば
とある。T[6, di] が示す位置の画素を見ても有効画素にはならないのだ。nv が6の時は for を continue しても良い。または nv が6の時は7として処理しても良い。 つまり for の 条件を nv < 7 とする事もできる。
次に判定する画素の方向を ni とすると、判定する画素の座標を決めるために if や switch で ni = 7 なら X座標は -1 を加算, Y座標は変わらず、 ni = 0 なら X座標は変わらず, Y座標は 1 を加算と処理しても良いのだが、X方向変数[ni]とY方向変数[ni]で加減算の値が得られると、処理の記述が簡素化する。 そこで加算ベクトルの変数を
this.addx = [ -1, 0, 1, 1, 1, 0, -1, -1 ]; this.addy = [ 1, 1, 1, 0, -1, -1, -1, 0 ];
として配列を持つ。
これで、変数の役者は揃った。ソースにすると下記のようになる。this.EggeData については次節で説明しよう。
// 輪郭線追跡変数初期化
var px = St.x;
var py = St.y;
var di = 1;
// 輪郭線追跡処理
do {
for (var nv = 0; nv < 8; nv++) {
// 一つ前の輪郭の向きがーーー
// 輪郭を検索する向きの値がーーー
// 左?左下?それともここか?
// 決まったら赤点打てよ for break じゃ
}
// 最後にスタート地点に戻ったら処理は終了です。
} while (px != St.x || py != St.y);
 左表は di と nv の組み合わせを示している。この表をTとすると、T[nv, di] は次に判定する画素の方向を示す。T[0, 0] は7だから左の画素を見る。
T[0, 1] は0だから左下の画素を見ると言った具合だ。有効画素であった場合は、di に nv を記憶し for ループを脱出する。
左表は di と nv の組み合わせを示している。この表をTとすると、T[nv, di] は次に判定する画素の方向を示す。T[0, 0] は7だから左の画素を見る。
T[0, 1] は0だから左下の画素を見ると言った具合だ。有効画素であった場合は、di に nv を記憶し for ループを脱出する。左表の二次元テーブルを変数にして処理したら、次の判定画素を確定する事は可能だ。しかし表を見ると直感的に何かしらの規則性があるように感じる。 つまり表を変数にしなくても計算により導き出せるのではないか?と感じる。表の要素は何かを8で割った時の余りになるような気がする。8方向は 0~7 の値をとるからだ。 (nv + di + 7) % 8 ならどうだろう?おぉズバリじゃないか。これで表の変数は不要だ。
ところで参考にしたページによれば
一つ前の輪郭の向きから時計回りに3つ分の向きには輪郭が存在しない。
とある。T[6, di] が示す位置の画素を見ても有効画素にはならないのだ。nv が6の時は for を continue しても良い。または nv が6の時は7として処理しても良い。 つまり for の 条件を nv < 7 とする事もできる。
次に判定する画素の方向を ni とすると、判定する画素の座標を決めるために if や switch で ni = 7 なら X座標は -1 を加算, Y座標は変わらず、 ni = 0 なら X座標は変わらず, Y座標は 1 を加算と処理しても良いのだが、X方向変数[ni]とY方向変数[ni]で加減算の値が得られると、処理の記述が簡素化する。 そこで加算ベクトルの変数を
this.addx = [ -1, 0, 1, 1, 1, 0, -1, -1 ]; this.addy = [ 1, 1, 1, 0, -1, -1, -1, 0 ];
として配列を持つ。
これで、変数の役者は揃った。ソースにすると下記のようになる。this.EggeData については次節で説明しよう。
// 起点が決定済み... if (St) { // 輪郭線追跡変数初期化 var px = St.x; var py = St.y; var di = 1; var Ev = this.addx.length - 1; // 輪郭点記憶用配列を追加 this.EggeData.push({ ary:new Array() }); // 輪郭点記憶用配列の最後の指標を得る var idxEgge = this.EggeData.length - 1; // 輪郭線追跡処理 do { // 一つ前の輪郭の向きから時計回りに3つ分の向きには輪郭が存在しない for (var nv = 0; nv < Ev; nv++) { // nv が6の時は7として処理する var ni = (nv == (Ev - 1) ? Ev : (nv + di + Ev) % this.addx.length); var nx = px + this.addx[ni]; var ny = py + this.addy[ni]; // 画素の座標が画像の範囲内にあるなら... if (nx >= 0 && nx < w && ny >= 0 && ny < h) { // 有効画素であるなら... if (this.IsOpaquePixcel(inData, nx, ny, w)) { // 輪郭点を記憶 this.EggeData[idxEgge].ary.push({ nx:nx, ny:ny }); // 画素の位置を記憶して次の探索点へ px = nx; py = ny; di = ni; break; } } } // 最後にスタート地点に戻ったら処理は終了です。 } while (px != St.x || py != St.y); }
4 私を分かつもの
有耶無耶にしていた連結部分について話そう。部分の「部」の字を画像にして輪郭追跡すると3個の輪郭になる。これを3個の連結部分と言う。つまり連結は塊(輪郭で囲んだ部分)を示し、
この塊の個々の事を連結部分と言うのだ。よって連結部分は1個以上存在する。
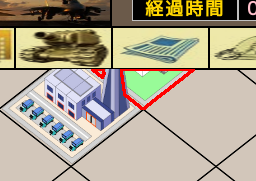 左図は左下からの施設の煙突によって、2個の連結部分になった状態である。施設を表示する窓をマウスで引きずるとスクロールが可能なので、スクロールした位置によっては左図のような
状態もあり得るのだ。またスクロールしない状況においても、東京スカイツリーのような高い(長い)建物があれば、連結部分が複数になる可能性もある。1回の輪郭追跡では左図のようなセレクタの
表現は出来ない。考えられる処理としては輪郭追跡を再帰する事だ。そこで登場するのが this.EggeData 変数だ。前節で示したソースでは、this.EggeData の配列の要素に連結部分を記憶している。
この要素は更に配列になっていて、輪郭の画素の座標を記憶する。連結部分が出揃った後に赤い画素を打ちセレクタを表現する。
左図は左下からの施設の煙突によって、2個の連結部分になった状態である。施設を表示する窓をマウスで引きずるとスクロールが可能なので、スクロールした位置によっては左図のような
状態もあり得るのだ。またスクロールしない状況においても、東京スカイツリーのような高い(長い)建物があれば、連結部分が複数になる可能性もある。1回の輪郭追跡では左図のようなセレクタの
表現は出来ない。考えられる処理としては輪郭追跡を再帰する事だ。そこで登場するのが this.EggeData 変数だ。前節で示したソースでは、this.EggeData の配列の要素に連結部分を記憶している。
この要素は更に配列になっていて、輪郭の画素の座標を記憶する。連結部分が出揃った後に赤い画素を打ちセレクタを表現する。
再帰するためには、一つの連結部分を処理した後に、その連結部分を黒の完全透明にして繰り返す必要がある。さもなければ同じ連結部分が処理されて永久ループに陥る。 近傍探索を行う最初の画素が見つからない状態になるまで再帰を繰り返すと、全ての連結部分を列挙する事ができると言う算段だ。
連結部分を黒の完全透明にするために、当初は canvas の clip メソッドと fill メソッドで行おうとしたのだが、 アンチエイリアスの処理を 行っているようで黒の完全透明にする事が出来なかった。ならば画素を直接操作して連結部分を黒の完全透明にしようじゃないか。考え方を下記に示す。
1) 連結部分の配列をコピーして新たな配列を作る。
2) 上記の配列をソートする。
3) 上記の配列から水平ラインを追って黒の完全透明にする。
この考え方に従って実装したソースを下記に示す。inp.data[ix + 0] = inp.data[ix + 1] = inp.data[ix + 2] = inp.data[ix + 3] = 0; は RGBA を設定している。
 左図は左下からの施設の煙突によって、2個の連結部分になった状態である。施設を表示する窓をマウスで引きずるとスクロールが可能なので、スクロールした位置によっては左図のような
状態もあり得るのだ。またスクロールしない状況においても、東京スカイツリーのような高い(長い)建物があれば、連結部分が複数になる可能性もある。1回の輪郭追跡では左図のようなセレクタの
表現は出来ない。考えられる処理としては輪郭追跡を再帰する事だ。そこで登場するのが this.EggeData 変数だ。前節で示したソースでは、this.EggeData の配列の要素に連結部分を記憶している。
この要素は更に配列になっていて、輪郭の画素の座標を記憶する。連結部分が出揃った後に赤い画素を打ちセレクタを表現する。
左図は左下からの施設の煙突によって、2個の連結部分になった状態である。施設を表示する窓をマウスで引きずるとスクロールが可能なので、スクロールした位置によっては左図のような
状態もあり得るのだ。またスクロールしない状況においても、東京スカイツリーのような高い(長い)建物があれば、連結部分が複数になる可能性もある。1回の輪郭追跡では左図のようなセレクタの
表現は出来ない。考えられる処理としては輪郭追跡を再帰する事だ。そこで登場するのが this.EggeData 変数だ。前節で示したソースでは、this.EggeData の配列の要素に連結部分を記憶している。
この要素は更に配列になっていて、輪郭の画素の座標を記憶する。連結部分が出揃った後に赤い画素を打ちセレクタを表現する。再帰するためには、一つの連結部分を処理した後に、その連結部分を黒の完全透明にして繰り返す必要がある。さもなければ同じ連結部分が処理されて永久ループに陥る。 近傍探索を行う最初の画素が見つからない状態になるまで再帰を繰り返すと、全ての連結部分を列挙する事ができると言う算段だ。
連結部分を黒の完全透明にするために、当初は canvas の clip メソッドと fill メソッドで行おうとしたのだが、 アンチエイリアスの処理を 行っているようで黒の完全透明にする事が出来なかった。ならば画素を直接操作して連結部分を黒の完全透明にしようじゃないか。考え方を下記に示す。
1) 連結部分の配列をコピーして新たな配列を作る。
2) 上記の配列をソートする。
3) 上記の配列から水平ラインを追って黒の完全透明にする。
この考え方に従って実装したソースを下記に示す。inp.data[ix + 0] = inp.data[ix + 1] = inp.data[ix + 2] = inp.data[ix + 3] = 0; は RGBA を設定している。
// 起点が決定済み... if (St) { // 前節のソース部 do { // 前節のソース部参照されたし } while (px != St.x || py != St.y); // 輪郭点記憶用配列をコピー var ary = $.extend(true, [], this.EggeData[idxEgge].ary); // ソート ary.sort(function(a, b) { if (a.ny == b.ny) return (a.nx == b.nx ? 0 : (a.nx < b.nx ? -1 : 1)); else return (a.ny < b.ny ? -1 : 1); }); // 連結部分を黒の完全透明にする for (var idx = 0; idx < ary.length; idx++) { var ix = (ary[idx].ny * inp.width + ary[idx].nx) * 4; inp.data[ix + 0] = inp.data[ix + 1] = inp.data[ix + 2] = inp.data[ix + 3] = 0; // 水平ラインを処理する if (idx + 1 < ary.length) { if (ary[idx].ny == ary[idx + 1].ny) { for (var x = ary[idx].nx + 1; x <= ary[idx + 1].nx; x++) { var ix = (ary[idx].ny * inp.width + x) * 4; inp.data[ix + 0] = inp.data[ix + 1] = inp.data[ix + 2] = inp.data[ix + 3] = 0; } } } } // 連結部分の黒の完全透明をかぶせる ctxRst.putImageData(inp, this.EggeDx, this.EggeDy, 0, 0, this.EggeCx, this.EggeCy); // 輪郭追跡を再帰する this.PutPixcelEgge(ctxRst, dx, dy, cx, cy, sz); }ついでにセレクタの赤点を打つ部分も掲げておく。これでセレクタ表現ができた(^^)v
// 輪郭描画 clsMath.prototype.DrawPixcelEgge = function(ctxRst) { // 結果出力用オブジェクトを生成 var out = ctxRst.createImageData(this.EggeCx, this.EggeCy); // 輪郭点を打つ for (var idx = 0; idx < this.EggeData.length; idx++) { for (var pos = 0; pos < this.EggeData[idx].ary.length; pos++) { this.PutRedPixcel(out.data, this.EggeData[idx].ary[pos].nx, this.EggeData[idx].ary[pos].ny, out.width, out.height); } } // 輪郭をかぶせる ctxRst.putImageData(out, this.EggeDx, this.EggeDy, 0, 0, this.EggeCx, this.EggeCy); } // 赤い画素を設定する clsMath.prototype.PutRedPixcel = function(otData, x, y, w, h) { for (var ay = -1; ay < 2; ay++) { for (var ax = -1; ax < 2; ax++) { var py = y + ay; var px = x + ax; // 赤色の画素に設定 if (py >= 0 && py < h) { if (px >= 0 && px < w) { var idx = (py * w + px) * 4; otData[idx + 0] = otData[idx + 3] = 255; otData[idx + 1] = otData[idx + 2] = 0; } } } } }