君は危険を冒して冒険する?それとも探検する?
1 クエストなんですか?
「お前なら行けるさ♪トム♪誰よりも遠くへ♪地平線の彼方で♪待っている♪すばらしい冒険が♪」これはトムソーヤの冒険の主題曲のフレーズだ。冒険と言う響きには「わくわくどきどき」
感があるよね。ゲームの世界ではクエストなる語が用いられる事が多いようだ。クエストとは、本来は「探求や探索」を意味する単語だそうで、外来語と言うかカタカナ語と言うか、それらで
表現する事が好きな人たちが多い世界だ。尤もこの風潮はゲームの世界に限った事ではないがね。私のゲームでは「探検」を用いる。探検の意味は「未知の地域に(危険をおかして)踏み込んで、
そこを調べること」とある。ここは名は体を表す表現を採用した。
クエストと言えば、ドラゴンクエストと言う有名なゲームがあるそうじゃないか。って私はやった事がない(__!) RPG の大衆化に成功した作品と言うだけあって、シナリオ、キャラクターデザイン、 音楽、プログラミングには錚錚たる人物が並ぶ。CDシアター版ってのもあるらしい。ドラマ(アニメ)らしい。見たことはないぞ(__!) これも錚錚たる声優たちが抜擢されている。 この作品からゲーム界隈ではクエスト流行りになったのだろうか。
クエストにミッション(使命や任務)の意味を含ませるゲームもあるようだ。さらにクエストミッションなんて語もあるぞ。ゲームの分際で俺様に○○を達成しろと、言ってくるのだ(^^!) まぁゲームなんだし面白ければ何だってありなんだけど、世の中で新たな語が生まれる度に、それ知らないの?って言ってくる輩がいるのも、何だかなぁと思ってしまう(^^) ちなみに私はゲームを作るまでは NPC(ノンプレイヤーキャラクター)と言う用語も知らなかった。用語を知らずともゲームは作れる事を実証したかった、なんて事は、ないない(^^)
さて前置きはこれくらいにして、今回は最短経路の話である。
クエストと言えば、ドラゴンクエストと言う有名なゲームがあるそうじゃないか。って私はやった事がない(__!) RPG の大衆化に成功した作品と言うだけあって、シナリオ、キャラクターデザイン、 音楽、プログラミングには錚錚たる人物が並ぶ。CDシアター版ってのもあるらしい。ドラマ(アニメ)らしい。見たことはないぞ(__!) これも錚錚たる声優たちが抜擢されている。 この作品からゲーム界隈ではクエスト流行りになったのだろうか。
クエストにミッション(使命や任務)の意味を含ませるゲームもあるようだ。さらにクエストミッションなんて語もあるぞ。ゲームの分際で俺様に○○を達成しろと、言ってくるのだ(^^!) まぁゲームなんだし面白ければ何だってありなんだけど、世の中で新たな語が生まれる度に、それ知らないの?って言ってくる輩がいるのも、何だかなぁと思ってしまう(^^) ちなみに私はゲームを作るまでは NPC(ノンプレイヤーキャラクター)と言う用語も知らなかった。用語を知らずともゲームは作れる事を実証したかった、なんて事は、ないない(^^)
さて前置きはこれくらいにして、今回は最短経路の話である。
2 歩くのは好きですか?
当ゲームでは探検画面にて「宝箱をクリックすると探検者が勝手に歩いて行って開封する」事にした。歩くのが大好きな人は、たまに遠回りしたりもするだろう。だけど大抵の人は近道を好む。
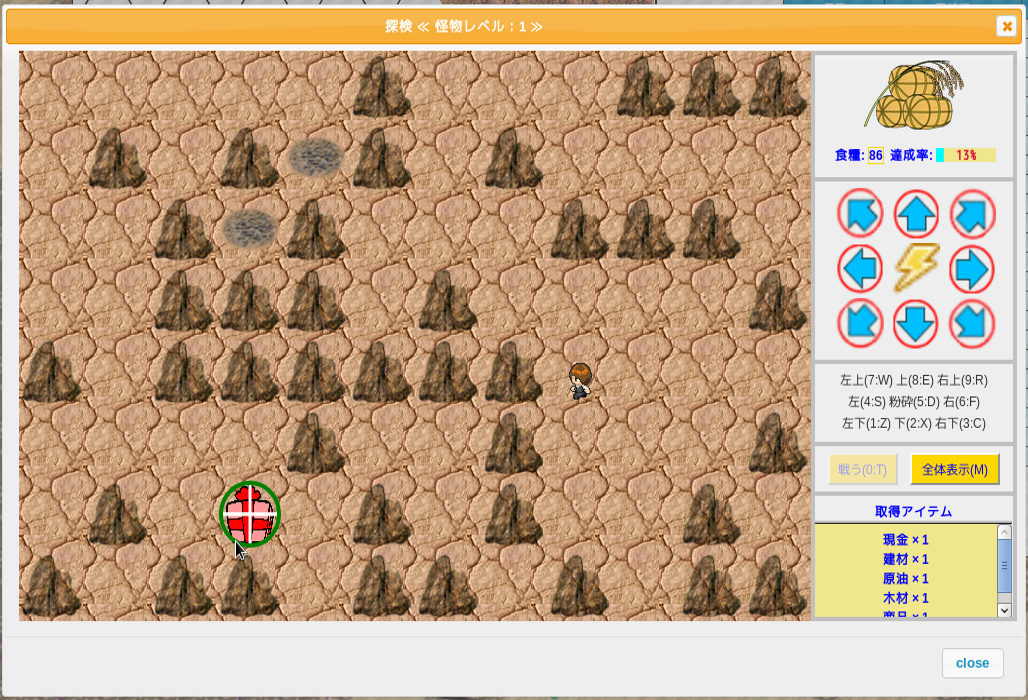
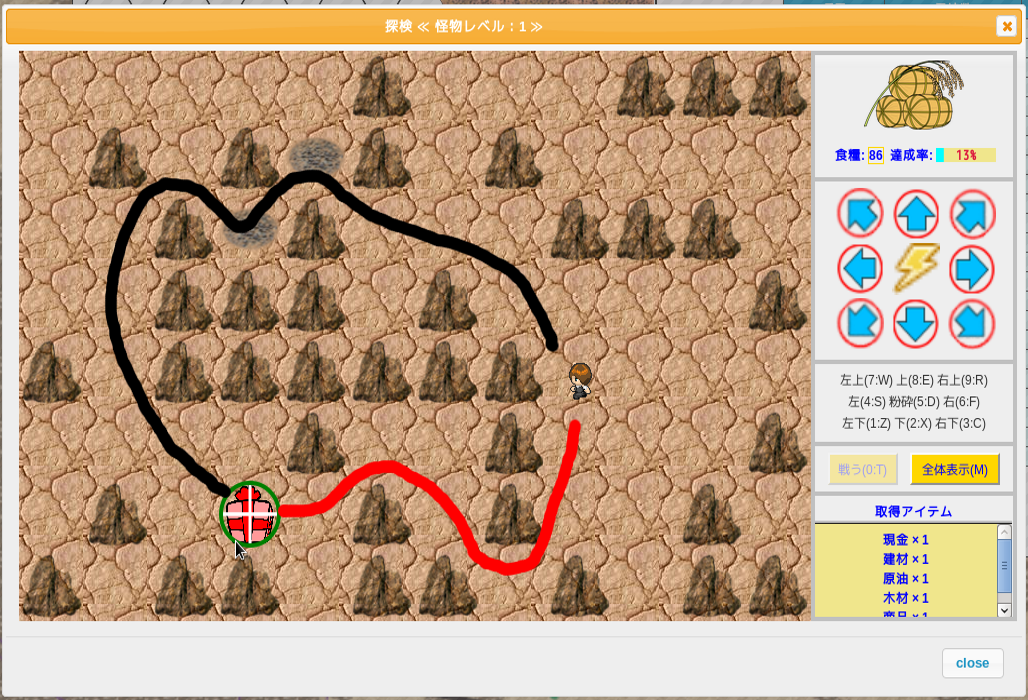 左側の図は赤い宝箱をクリックする様子を示している。この赤い宝箱まで歩いて行く経路は複数存在する。右側の図で示した黒線の経路もあれば、もっと遠回りする経路もあるだろう。その複数の
経路の中で最短の経路は赤線で示した経路である。なお障害物となる岩は、探検画面を開く度に乱数で配置を決める。よって同じ配置になる事は、ほとんどない。おそらく限りなくゼロに近いだろう。
左側の図は赤い宝箱をクリックする様子を示している。この赤い宝箱まで歩いて行く経路は複数存在する。右側の図で示した黒線の経路もあれば、もっと遠回りする経路もあるだろう。その複数の
経路の中で最短の経路は赤線で示した経路である。なお障害物となる岩は、探検画面を開く度に乱数で配置を決める。よって同じ配置になる事は、ほとんどない。おそらく限りなくゼロに近いだろう。
岩は粉砕可能であり、粉砕した箇所は歩く事ができる。また開封した宝箱があった箇所も、開封後は歩く事が出来る。さらに探検者の動きはプレイヤーが決定するので、あらかじめ最短経路を計算 しておく事はできない。つまりクリック時点で最短経路を計算する必要がある。探検者が勝手に歩くのは、宝箱だけに限らない。移動して欲しい場所をクリックしたなら、勝手に歩いて行く。 歩いて行った後に、クリックした対象が宝箱であれば自動的に開封するし、障害物であれば自動的に粉砕する。また単なる地べたなら歩いて行くだけだ。
任意のクリックした場所までの最短経路を計算し、その経路をたどるように探検者を歩かせようと言う魂胆だ。最短経路の計算はサーバで行い、探検者の歩行はクライアント(ブラウザ)で行う。 サーバ側の言語は PHP を用いる。

 左側の図は赤い宝箱をクリックする様子を示している。この赤い宝箱まで歩いて行く経路は複数存在する。右側の図で示した黒線の経路もあれば、もっと遠回りする経路もあるだろう。その複数の
経路の中で最短の経路は赤線で示した経路である。なお障害物となる岩は、探検画面を開く度に乱数で配置を決める。よって同じ配置になる事は、ほとんどない。おそらく限りなくゼロに近いだろう。
左側の図は赤い宝箱をクリックする様子を示している。この赤い宝箱まで歩いて行く経路は複数存在する。右側の図で示した黒線の経路もあれば、もっと遠回りする経路もあるだろう。その複数の
経路の中で最短の経路は赤線で示した経路である。なお障害物となる岩は、探検画面を開く度に乱数で配置を決める。よって同じ配置になる事は、ほとんどない。おそらく限りなくゼロに近いだろう。
岩は粉砕可能であり、粉砕した箇所は歩く事ができる。また開封した宝箱があった箇所も、開封後は歩く事が出来る。さらに探検者の動きはプレイヤーが決定するので、あらかじめ最短経路を計算 しておく事はできない。つまりクリック時点で最短経路を計算する必要がある。探検者が勝手に歩くのは、宝箱だけに限らない。移動して欲しい場所をクリックしたなら、勝手に歩いて行く。 歩いて行った後に、クリックした対象が宝箱であれば自動的に開封するし、障害物であれば自動的に粉砕する。また単なる地べたなら歩いて行くだけだ。
任意のクリックした場所までの最短経路を計算し、その経路をたどるように探検者を歩かせようと言う魂胆だ。最短経路の計算はサーバで行い、探検者の歩行はクライアント(ブラウザ)で行う。 サーバ側の言語は PHP を用いる。
3 信じる道を行きますか?
最短経路の計算アルゴリズムにA*(A-star, エースターを用いる。参考にしたページ(以降はSPと呼ぶ)には、詳細な説明があり
アルゴリズムの実装の擬似コーディングが掲載されている。詳細な説明と言っても、私の頭では理解不能だ(^^) はっきり言って、このアルゴリズムで最短経路が導き出せるのか?分からない(TT)
しかし探索の過程を示した動画を見て、何となく雰囲気は飲み込めた。きっと出きるに違いない。ここは信じた道を行こう。
SP は2017年3月13日現在のものだ。記述に誤りがあると思われるため、更新される可能性がある。画像として引用しておく。

目標までの最短距離と言えば、出発点と目標点を結ぶ線分になる。SP の動画でも線分を辿って行く。障害物に出会ったら次の最短はどこだ?みたいに計算しているように見える。 SP の記述によると
探検画面は、表示はしていないが四角形の格子状になっている。位置を表すには行番号と列番号を使用する。実際の座標(四角形の左上)は、列番号×格子の幅、行番号×格子の高さとなる。 距離のコストは行列の番号で計算する。線分の距離なら、√(水平距離の二乗+垂直距離の二乗)で求まる。それでは、SP のアルゴリズムの流れに従って道を進んで行こう。
SP は2017年3月13日現在のものだ。記述に誤りがあると思われるため、更新される可能性がある。画像として引用しておく。

目標までの最短距離と言えば、出発点と目標点を結ぶ線分になる。SP の動画でも線分を辿って行く。障害物に出会ったら次の最短はどこだ?みたいに計算しているように見える。 SP の記述によると
スタートノードから、あるノード n を通って、ゴールノードまでたどり着くときの最短経路を考える。このときこの最短経路のコストを f* (n) とおくと云々とある。コストと言う言葉が出てきた。これは距離をコストとするか、時間をコストとするか、料金をコストとするかで、最短距離、最短時間、最低料金の探索に応用可能と言う事だ。 ここでは、距離がコストである。SP ではコストの推定値を返すヒューリスティック関数なるものが必要だと言っている。
探検画面は、表示はしていないが四角形の格子状になっている。位置を表すには行番号と列番号を使用する。実際の座標(四角形の左上)は、列番号×格子の幅、行番号×格子の高さとなる。 距離のコストは行列の番号で計算する。線分の距離なら、√(水平距離の二乗+垂直距離の二乗)で求まる。それでは、SP のアルゴリズムの流れに従って道を進んで行こう。
4 出発点ノードは何にしますか?
SP のアルゴリズムの流れの1番目
スタートノードは探検者がいる位置である。優先度つきキューだが、何の事か分からない。最小値を即座に求められるような構造にしろと言うことか? しかし、着目ノードがリスト内に存在するか確かめる操作が常に必要なので、行列番号をキーとするハッシュテーブルの方が効率がよいだろう。必要な関数のソースを下記に示す。 putNode 関数の oHash はOPENリスト、cHash はCLOSEリストである。登録は置換も含む。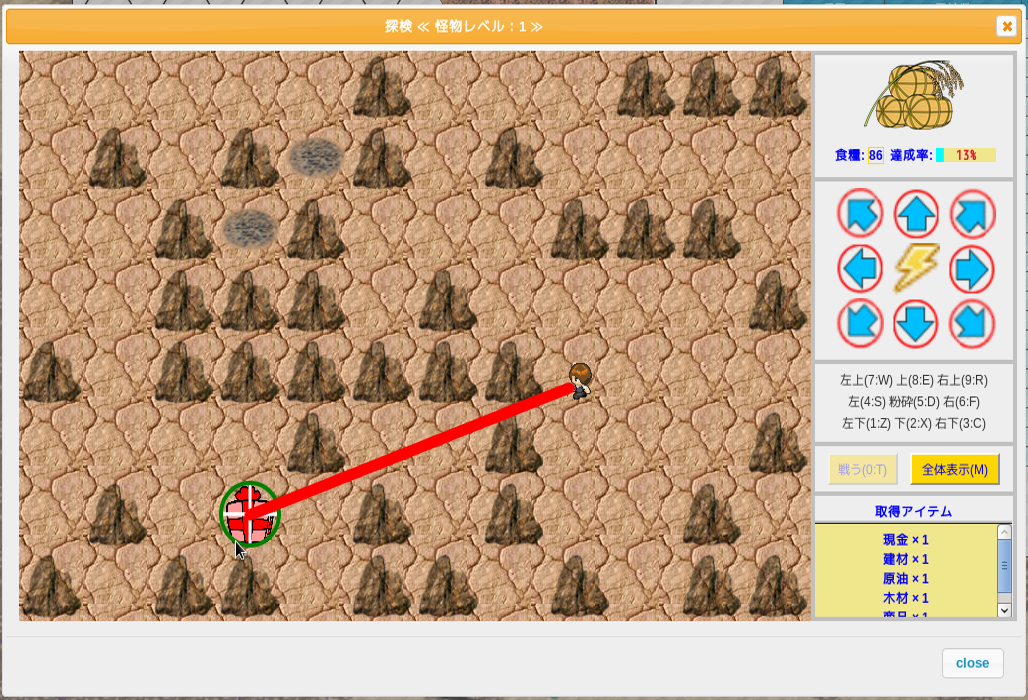 出発ノードのコストは探検者と対象物の距離コストを設定する。左図の赤線部分だ。
出発ノードのコストは探検者と対象物の距離コストを設定する。左図の赤線部分だ。
SP のアルゴリズムの流れの2番目
しかし当ゲームではゴールは必ず一つなので、上記の内容は不要である。よってアルゴリズムの流れの1~3の実装は下記になる。
1.スタートノードを作成する。また計算中のノードを格納しておくための優先度つきキュー OPENリストと、計算済みのノードを格納しておくCLOSEリストを用意する。 (名前は「リスト」だが、これらの実際のデータ構造は必ずしも連結リストである必要はない。)とある。
スタートノードは探検者がいる位置である。優先度つきキューだが、何の事か分からない。最小値を即座に求められるような構造にしろと言うことか? しかし、着目ノードがリスト内に存在するか確かめる操作が常に必要なので、行列番号をキーとするハッシュテーブルの方が効率がよいだろう。必要な関数のソースを下記に示す。 putNode 関数の oHash はOPENリスト、cHash はCLOSEリストである。登録は置換も含む。
// 経路上のノード生成 private function NewNode($parent, $row, $col) { $key = substr('0000'.$row, -4).substr('0000'.$col, -4); $new = array('key' => $key, 'row' => $row, 'col' => $col, 'cost' => 0, 'parent' => $parent); return $new; } // ノードを登録する private function putNode($node, $flgOpen) { if ($flgOpen) $this->oHash[$node['key']] = $node; else $this->cHash[$node['key']] = $node; } // 推定コスト計算 ヒューリスティック関数 // 二つの指定ノードの推定コストを計算する // この関数が最短経路を選択する肝になる private function getHeuristicCost($node, $next) { // 二つのノードの行列の差を得る $a = $node['row'] - $next['row']; $b = $node['col'] - $next['col']; // 二つのノードのコストを計算する $c = sqrt(($a * $a) + ($b * $b)); // 結果を返す return $c; }
 出発ノードのコストは探検者と対象物の距離コストを設定する。左図の赤線部分だ。
出発ノードのコストは探検者と対象物の距離コストを設定する。左図の赤線部分だ。SP のアルゴリズムの流れの2番目
2.ゴールは必ずしも1つである必要はないので、ゴール条件を満たすノード集合を G と呼ぶことにする。とある。
しかし当ゲームではゴールは必ず一つなので、上記の内容は不要である。よってアルゴリズムの流れの1~3の実装は下記になる。
// 1.初期化 出発点ノードとゴールノードを作成する $sNode = $this->NewNode(null, $StRow, $StCol); $gNode = $this->NewNode($sNode, $EdRow, $EdCol); // 2.出発点ノードをOpenリストに追加する、このとき g*(S) = 0 であり f*(S) = h*(S) となる $sNode['cost'] = $this->getHeuristicCost($sNode, $gNode); $this->putNode($sNode, true);これで探索ループの前段部は出来た。
5 終了条件は何ですか?
SP のアルゴリズムの流れの4番目
4.Openリストが空なら探索は失敗とする(開始からゴールにたどり着くような経路が存在しなかったことになる)。とある。 飛んで SP のアルゴリズムの流れの8番目
8.3 以降を繰り返す。とある。まず「Openリストが空なら探索は失敗とする」とあるが意味不明である。「Openリストが空なら探索を終了する」と解釈すると辻褄があう。また、「3 以降を繰り返す。」と あるが、SP のアルゴリズムの流れの3番目は
3.スタートノードをOpenリストに追加する、このとき <省略> また Closeリストは空にする。とある。これはループに入る前の段階の話なので、SP のアルゴリズムの流れの8番目は「4 以降を繰り返す。」が正しい。よってループ処理の実装は下記になる。
// 3.Openリストが空になるまでループ
while (count($this->oHash) > 0) {
// SP のアルゴリズムの流れの5、6、7を行う
}
6 最小のノードは何ですか?
SP のアルゴリズムの流れの5番目を読み替えて
5.Openリストに格納されているノードの内、最小の距離コストを持つノード n を取り出す。最小の距離コストを持つノードが複数ある場合、タイブレーク手法によりどれかのノードを選択する。と解釈する。タイブレーク手法なんて難しい言葉がでてきたなぁ(^^) まぁ同点なんだけど何か理由を付けて、どれかを勝たせろと言う事だ。ここは最初に見つかったノードを選択する。 最小の距離コストを持つノード n を取り出す関数を下記に示す。Openリストはキューにしろとあったので、取り出したら削除する。キュー操作の POP に相当する。
// 最小コストのノードを得る private function getMinCostNode() { $mNode = null; // Openリストがあるなら... if (count($this->oHash) > 0) { // ダミーノードを生成する $mNode = $this->NewNode(null, 0, 0); $mNode['cost'] = PHP_INT_MAX; // コストの最小値を探索する foreach($this->oHash as $node) { if ($node['cost'] < $mNode['cost']) $mNode = $node; } // ハッシュを削除 unset($this->oHash[$mNode['key']]); } // 結果を返す return $mNode; }SP のアルゴリズムの流れの5番目の実装は下記になる。
// Openリストに格納されているノードの内、最小の距離コストを持つノード n を取り出す。 $node = $this->getMinCostNode();
7 ゴールに到着しましたか?
SP のアルゴリズムの流れの6番目を読み替えて
6.ゴールに到着したら探索を終了する。それ以外の場合は n を Close リストに移す。と解釈する。よって SP のアルゴリズムの流れの6番目の実装は下記になる。
// ゴールであるなら探索を終了する
if ($node['row'] == $EdRow && $node['col'] == $EdCol) {
$gNode = $node;
break;
}
// ゴール以外の場合は n を Close リストに移す。
$this->putNode($node, false);
8 またしても八近傍ですか?
SP のアルゴリズムの流れの7番目
7.n に隣接している全てのノード(ここでは隣接ノードを m とおく)に対して以下の操作を行うとある。つまり、m は着目ノードの八近傍の事である。最初の着目ノードは探検者がいる場所(出発点ノード)だ。この部分の実装は下記になる。
// n に隣接している全てのノード(時計回り8方向の隣接ノードを m とおく)に対して以下の操作を行う
for ($v = 0; $v < 8; $v++) {
// 着目ノードの座標を得る
$r = $node['row'];
$c = $node['col'];
// 北、北東、北西
if ($v == 0 || $v == 1 || $v == 7)
$r--;
// 南東、南、南西
if ($v == 3 || $v == 4 || $v == 5)
$r++;
// 北東、東、南東
if ($v == 1 || $v == 2 || $v == 3)
$c++;
// 南西、西、北西
if ($v == 5 || $v == 6 || $v == 7)
$c--;
// マップ範囲内にあるならば...
if (isset($map[$r]) && isset($map[$r][$c])) {
// SP のアルゴリズムの流れの7番目の 7.1 と 7.2 の処理を行う
}
}
9 遠ざかってはいけないのですか?
SP のアルゴリズムの流れの7番目の1
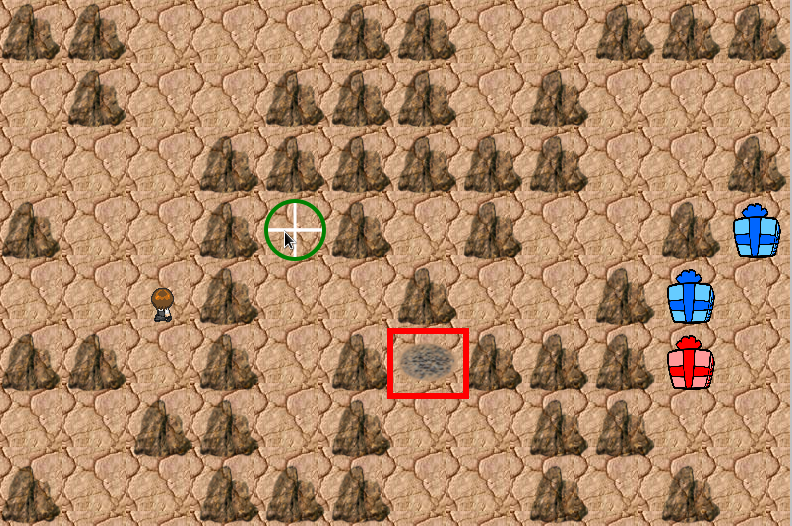 n はOpenリストから取り出した距離コストが最小のノードである。m は n の隣接ノードだ。COST(n,m) は1または√2の値になる。h(m) は隣接ノードとゴールノードとの距離コストである。
これを加算するのは、ゴールから遠ざかる m ノードはコストを高くしようと言う事だ。これは大抵の場合は正しいだろう。しかし当ゲームにおいては不都合が生じる。
n はOpenリストから取り出した距離コストが最小のノードである。m は n の隣接ノードだ。COST(n,m) は1または√2の値になる。h(m) は隣接ノードとゴールノードとの距離コストである。
これを加算するのは、ゴールから遠ざかる m ノードはコストを高くしようと言う事だ。これは大抵の場合は正しいだろう。しかし当ゲームにおいては不都合が生じる。
左図を見て欲しい。h(m) を加算すると探検者は上に移動して終わりになる。これは上のノードとゴールノードの距離コストが最小となるからだ。ところが h(m) を加算しなければ、 探検者は指定の位置まで歩行するのだ。指定した位置が到達可能な場所である事は、赤枠で囲んだ地べたを見てもらえば分かる。この赤枠の箇所は岩を粉砕したか、 または宝箱を開封した事を示している。到達不能の場所なら粉砕または開封の操作が行えない。到達不能な場所は周囲を完全に障害物で囲まれた場所なのだ。
遠ざかる事を許す事で、探検者は障害物を回避して遠回りしながら、指定位置まで辿り着く。画面スクロールも頻繁に行われる。歩行する探検者を見ていると、頑張れと言いたくなるくらいだ(^^) 遠ざかる事を許して計算する事で、計算量は増えるだろうが、確実に障害物を回避して辿り着く事を優先し h(m) の加算は行わない事とする。
次に g(n) であるが、これはノードのデータの中に累計コストを保持しているので、それを使用する。g(n) = f(n) - h(n) で求める事が出きるとあるが、 遠ざかりを加算しないので減算も必要ない。
障害物があるノードは距離コストが高くなるように計算する。障害物の距離コストはいくらにするかだ。これは窓枠の行列の大きさがわかれば、√(行数の二乗+列数の二乗) +1 でよいだろう。 だが当ゲームの経路計算のクラスは、全体マップの大きさしか知らない。全体マップの大きさを採用しても良いのだが、ここは、$ObstacleCost = $this->ChipSize * $this->ChipSize; とする。 ChipSize はグリッドの四角形のサイズだ。66×66となる。窓枠サイズはこれより大きくはならない(と言うかしない)。窓枠の大きさは12×8だ。障害物の距離コストは、 出発点ノードとゴールノードの距離コストが取りうる最大値 √(12二乗+8二乗) より大きいなら、問題ない。
実装は下記のようになる。
7.1 g(n) + COST(n,m) + h(m) を計算するの部分の実装を考えてみる。 SP のアルゴリズムを端的に示すと、「推定コストの総和が最小の値になるものを最短経路にする」と言う事だ。そして推定値を返すのがヒューリスティック関数である。それを getHeuristicCost として実装した。
 n はOpenリストから取り出した距離コストが最小のノードである。m は n の隣接ノードだ。COST(n,m) は1または√2の値になる。h(m) は隣接ノードとゴールノードとの距離コストである。
これを加算するのは、ゴールから遠ざかる m ノードはコストを高くしようと言う事だ。これは大抵の場合は正しいだろう。しかし当ゲームにおいては不都合が生じる。
n はOpenリストから取り出した距離コストが最小のノードである。m は n の隣接ノードだ。COST(n,m) は1または√2の値になる。h(m) は隣接ノードとゴールノードとの距離コストである。
これを加算するのは、ゴールから遠ざかる m ノードはコストを高くしようと言う事だ。これは大抵の場合は正しいだろう。しかし当ゲームにおいては不都合が生じる。左図を見て欲しい。h(m) を加算すると探検者は上に移動して終わりになる。これは上のノードとゴールノードの距離コストが最小となるからだ。ところが h(m) を加算しなければ、 探検者は指定の位置まで歩行するのだ。指定した位置が到達可能な場所である事は、赤枠で囲んだ地べたを見てもらえば分かる。この赤枠の箇所は岩を粉砕したか、 または宝箱を開封した事を示している。到達不能の場所なら粉砕または開封の操作が行えない。到達不能な場所は周囲を完全に障害物で囲まれた場所なのだ。
遠ざかる事を許す事で、探検者は障害物を回避して遠回りしながら、指定位置まで辿り着く。画面スクロールも頻繁に行われる。歩行する探検者を見ていると、頑張れと言いたくなるくらいだ(^^) 遠ざかる事を許して計算する事で、計算量は増えるだろうが、確実に障害物を回避して辿り着く事を優先し h(m) の加算は行わない事とする。
次に g(n) であるが、これはノードのデータの中に累計コストを保持しているので、それを使用する。g(n) = f(n) - h(n) で求める事が出きるとあるが、 遠ざかりを加算しないので減算も必要ない。
障害物があるノードは距離コストが高くなるように計算する。障害物の距離コストはいくらにするかだ。これは窓枠の行列の大きさがわかれば、√(行数の二乗+列数の二乗) +1 でよいだろう。 だが当ゲームの経路計算のクラスは、全体マップの大きさしか知らない。全体マップの大きさを採用しても良いのだが、ここは、$ObstacleCost = $this->ChipSize * $this->ChipSize; とする。 ChipSize はグリッドの四角形のサイズだ。66×66となる。窓枠サイズはこれより大きくはならない(と言うかしない)。窓枠の大きさは12×8だ。障害物の距離コストは、 出発点ノードとゴールノードの距離コストが取りうる最大値 √(12二乗+8二乗) より大きいなら、問題ない。
実装は下記のようになる。
// マップ範囲内にあるならば...
if (isset($map[$r]) && isset($map[$r][$c])) {
$m = $this->NewNode($node, $r, $c);
// $mCost = 累積距離コスト + COST(n,m) を計算する
// 累積距離コスト=現在着目しているノードのコスト=$node['cost']
// $aCost = COST(n,m) = ノード n から m へ移動するときのコスト
$aCost = $this->getHeuristicCost($node, $m);
$mCost = $node['cost'] + $aCost;
// m がゴールでなく障害物ならコストを大きくする
if (($r != $EdRow || $c != $EdCol) && $map[$r][$c] >= $this->Monster)
$mCost += $ObstacleCost;
// SP のアルゴリズムの流れの7番目の2の処理を行う
}
10 コストの小さいものに置き換えるのですか?
SP のアルゴリズムの流れの7番目の2
m の状態に応じて以下の操作を行うは、文字通りの実装を行う。
// m の状態に応じて以下の操作を行う
if (!isset($this->oHash[$m['key']]) && !isset($this->cHash[$m['key']])) {
// m が Openリストにも Closeリストにも含まれていない場合 f*(m) = f'(m)
$m['cost'] = $mCost;
// m を 登録する
$this->putNode($m, true);
}
else if (isset($this->oHash[$m['key']])) {
// m が Openリストにある場合登録済み m を得る
$m = $this->oHash[$m['key']];
// f'(m) < f*(m) であるなら
if ($mCost < $m['cost']) {
// f*(m) = f'(m) に置き換える
$m['cost'] = $mCost;
// m の親を n にする
$m['parent'] = $node;
// m を 置き換える
$this->putNode($m, true);
}
}
else if (isset($this->cHash[$m['key']])) {
// m が Closeリストにある場合登録済み m を得る
$m = $this->cHash[$m['key']];
// f'(m) < f*(m) であるなら
if ($mCost < $m['cost']) {
// m を Closeリストから削除
unset($this->cHash[$m['key']]);
// f*(m) = f'(m) とする
$m['cost'] = $mCost;
// m の親を n にする
$m['parent'] = $node;
// m を Openリストに追加する
$this->putNode($m, true);
}
}
11 これで私の行く道は決まりました
SP のアルゴリズムの流れの9番目を読み替えると
探索終了後、発見されたゴールノードの親を順次たどっていくと出発点からゴールまでの最短経路が得られる。となる。これの実装は下記になる。
// 経路結果変数
$route = array();
// 4.探索終了後、親を順次たどっていくと G から S までの最短経路が得られる。
while (isset($gNode['parent'])) {
$route[] = array('row' => $gNode['row'], 'col' => $gNode['col']);
$gNode = $gNode['parent'];
}
// 結果を返す
return $route;
これで最短経路探索は完了だ。最後にRPGクラスのソースを掲げておく。