ゲームエンジンを自作する
1 ゲームエンジンの生成
当ゲームでは、ゲームエンジンを自作し使用する。
1) なぜ自作するかについては、02 型に嵌めよう 5 ゲームエンジンで記述した。
2) 当ゲームに必要なゲームエンジンの機能は、02 型に嵌めよう 6 何が必要でございますか?で列挙した。
今回は、この方針に従い、ゲームエンジンの実装を記述していく。まず必要なのはゲームエンジンのクラスだ。これを clsGameUtl とする。clsGameEngine じゃないのか?って(__!)
それは、一般に言われるゲームエンジンの機能を、満たしているかと問われたら、胸を張ってゲームエンジンですとは、言えない自信のなさからだ(^^) ここは控えめのクラス名にしておく。
下記のクラスに何が必要かを考えながら、肉付けを行う。クラスを生成する引数として、ゲームのステージとなる div ブロックの id を渡す。HTML側にゲームのステージを記述する。
1) なぜ自作するかについては、02 型に嵌めよう 5 ゲームエンジンで記述した。
2) 当ゲームに必要なゲームエンジンの機能は、02 型に嵌めよう 6 何が必要でございますか?で列挙した。
今回は、この方針に従い、ゲームエンジンの実装を記述していく。まず必要なのはゲームエンジンのクラスだ。これを clsGameUtl とする。clsGameEngine じゃないのか?って(__!)
それは、一般に言われるゲームエンジンの機能を、満たしているかと問われたら、胸を張ってゲームエンジンですとは、言えない自信のなさからだ(^^) ここは控えめのクラス名にしておく。
下記のクラスに何が必要かを考えながら、肉付けを行う。クラスを生成する引数として、ゲームのステージとなる div ブロックの id を渡す。HTML側にゲームのステージを記述する。
// 省略時のゲームブロック要素ID var g_idStage = "#game-stage"; // ゲーム支援クラス var clsGameUtl = function(id) { };ゲームステージのスタイルには width と height を必須とする。オブジェクトを生成する場合は var gu = new clsGameUtl(); となる。 当然 div の id が game-stage でないなら、それを引数にして呼び出す。var gu = new clsGameUtl('#hoge') のようにだ。
<div id="game-stage" style="width:500px;height:500px;"> </div>
2 コンストラクタ
当ゲームエンジンでは、ゲームステージにアニメーションの枠(canvas) を追加する。アニメーションはコマ送りにより、動きを表現する。このコマ送りのタイミングを
requestAnimationFrameを使用して行う。また、途中でコマ送りを終了する場合には
cancelAnimationFrameを使用する。それでは clsGameUtl のコンストラクタに
window.requestAnimationFrame と window.cancelAnimationFrame の初期化を追加しよう。
// ゲーム支援クラス var clsGameUtl = function(id) { this.Element = (id || g_idStage); // three オブジェクトの引数の格納用 this.Core = { uFps:60 // 描画速度(frame per second) }; // インスタンス var inst = this; // フレーム処理を行う関数を得る if (!window.requestAnimationFrame) { window.requestAnimationFrame = ( window.webkitRequestAnimationFrame || window.mozRequestAnimationFrame || window.oRequestAnimationFrame || window.msRequestAnimationFrame || function(callback) { return window.setTimeout(callback, 1000 / inst.Core.uFps); } ); } // フレーム停止を行う関数を得る if (!window.cancelAnimationFrame) { window.cancelAnimationFrame = ( window.webkitCancelRequestAnimationFrame || window.mozCancelRequestAnimationFrame || window.oCancelRequestAnimationFrame || window.msCancelRequestAnimationFrame || function(id) { window.clearTimeout(id); } ); } };
3 レンダラの初期化
ゲームを実装するオブジェクトと、それを支援するゲームエンジンは別物だ。コマ送りのタイミングで呼び出す関数は、ゲームを実装するオブジェクトの内部にある。ゲームを実装するオブジェクトは
利用する側、ゲームエンジンは利用される側だ。コマ送りのタイミングで呼び出す関数のインスタンス(this)は、利用する側の方が都合が良い。そこで利用する側のオブジェクトを、ゲームエンジンに
記憶してもらうために、Initialize を呼び出してもらう事にする。
Initialize の呼び出しの目的は、レンダラの初期化である。 レンダラ(render) の原義 は「表現する、翻訳する、(脚本などを)上演する」などの意味だそうだ。当ゲームエンジンは、3Dにも対応する。3D部分の実装については、Three.js を使用する。Three のお決まりの処理として、 レンダラの初期化を行う必要がある。その処理を後で実装する。今は最低必要な機能に限定して話を進めていく。
Initialize の呼び出しの目的は、レンダラの初期化である。 レンダラ(render) の原義 は「表現する、翻訳する、(脚本などを)上演する」などの意味だそうだ。当ゲームエンジンは、3Dにも対応する。3D部分の実装については、Three.js を使用する。Three のお決まりの処理として、 レンダラの初期化を行う必要がある。その処理を後で実装する。今は最低必要な機能に限定して話を進めていく。
// ゲーム初期化 clsGameUtl.prototype.Initialize = function(Stage, NonRenderer, zIndex) { // 描画関数スタック this.aryLayer = []; // 当オブジェクトを使用するオブジェクトを記憶 this.Core.Stage = Stage; // レンダラの初期化 if (!NonRenderer) { // レンダラの初期化をあれやこれや行う } // 開始時間 this.StartTime = this.GetTime(); }
4 その他の最低限必要なメソッド
その他の最低限必要なメソッドを以下に列挙する。この時点のゲームエンジンのソースはこちらを参照されたい。
| メソッド | 内容 |
|---|---|
| CreateLayer | ゲームステージにアニメーションの枠(canvas) を追加する |
| Stop | ゲームを一時停止する |
| DoGame | ゲームループを開始する |
| DrawLayer | DoGame から呼び出しゲームを実装するオブジェクトが指定した関数を呼び出す |
| NewHiddenCanvas | 不可視の canvas を生成する |
| GetTime | Dateよりも詳細な時間を取得する |
| GetNextFrame | 次のフレーム番号を取得する |
| GetSize | ゲームステージのサイズを取得する |
| LoadImage | 画像のロードを行う |
5 ドット絵の足踏みから始めよう
さて、最低限の機能を実装したゲームエンジンを使用して、ドット絵の足踏みを表現して見よう。左図は RPG などで足踏や歩行を演出するドット絵だ。昨今は嬉しい事にネットを検索すると、
このようなドット絵を自動生成するツールを提供するサイトが多数ある。

左図は一つの画像であり、大きさは240×224だ。4行×6列のコマがある。よって1コマの大きさは40×56である。そして場面の数は8になる。 場面は主人公が足踏みする局面であり、下を向いて足踏みする場面、左下を向いて足踏みする場面、左を向いて足踏みする場面と続いて、全部で8方向の場面がある。 一つの場面を3コマで表現する。
サンプルページを作成した。サンプルのゲームは、主人公がシューティングする側でなく、 シューティングされる側である。ゲーム名をウニボールとしよう。ウニボールのソースをあげておく。 ウニボールのクラス名は clsSample01 だ。
clsSample01 のコンストラクタでゲームエンジンを生成する。その後に LoadImage で主人公とウニの画像をロードしている。 次に clsSample01 の Run メソッド内でキー入力イベントの設定、ゲームエンジン初期化、グリッドレイアの生成、主人公レイアの生成、ボールレイアの生成を行っている。 キー入力を受け持つ KeyDown メソッドでは、主人公の移動とゲーム開始の処理を行う。ゲーム開始の処理でゲームエンジンの DoGame を呼び出す。 これにより、clsSample01 の各レイアの処理を受け持つメソッドが呼び出される。
レイアの処理を受け持つメソッドは、1秒÷60=1000/60=約17m/s の速度で呼び出される。この速度で、主人公の足踏みを描画しても早すぎて見えない。 そこで、主人公レイアの描画を受け持つ EnterHero のメッソド内で、ゲームエンジンの GetNextFrame を呼び出している。これは、1コマの描画速度を調整する。 1コマの時間間隔とコマ数を与える事により、描画するコマの番号を返す。前回描画したコマの番号と取得したコマの番号が違うなら、描画を行う。 この調整により人間の目に見えるように表現するのだ。
ウニの速度の入力欄を儲けた。ウニボールのレイアのメソッド EnterBall では、この入力値を使用して GetNextFrame を呼び出している。 プレイヤーの好みの速度でウニが動く。反射神経の高いプレイヤーへの配慮だ。ウニが枠外に飛び出すと、ウニを避けたと言う事で得点を加算する。そして、枠内のランダムな位置にワープさせる。 主人公の位置とウニの位置が同じ、つまりウニに当たったら、ゲーム・オーバーとなる。枠内のランダムな位置の設定方法を工夫すると、面白みが増すだろう。ぜひ挑戦して頂きたい。

左図は一つの画像であり、大きさは240×224だ。4行×6列のコマがある。よって1コマの大きさは40×56である。そして場面の数は8になる。 場面は主人公が足踏みする局面であり、下を向いて足踏みする場面、左下を向いて足踏みする場面、左を向いて足踏みする場面と続いて、全部で8方向の場面がある。 一つの場面を3コマで表現する。
サンプルページを作成した。サンプルのゲームは、主人公がシューティングする側でなく、 シューティングされる側である。ゲーム名をウニボールとしよう。ウニボールのソースをあげておく。 ウニボールのクラス名は clsSample01 だ。
clsSample01 のコンストラクタでゲームエンジンを生成する。その後に LoadImage で主人公とウニの画像をロードしている。 次に clsSample01 の Run メソッド内でキー入力イベントの設定、ゲームエンジン初期化、グリッドレイアの生成、主人公レイアの生成、ボールレイアの生成を行っている。 キー入力を受け持つ KeyDown メソッドでは、主人公の移動とゲーム開始の処理を行う。ゲーム開始の処理でゲームエンジンの DoGame を呼び出す。 これにより、clsSample01 の各レイアの処理を受け持つメソッドが呼び出される。
レイアの処理を受け持つメソッドは、1秒÷60=1000/60=約17m/s の速度で呼び出される。この速度で、主人公の足踏みを描画しても早すぎて見えない。 そこで、主人公レイアの描画を受け持つ EnterHero のメッソド内で、ゲームエンジンの GetNextFrame を呼び出している。これは、1コマの描画速度を調整する。 1コマの時間間隔とコマ数を与える事により、描画するコマの番号を返す。前回描画したコマの番号と取得したコマの番号が違うなら、描画を行う。 この調整により人間の目に見えるように表現するのだ。
ウニの速度の入力欄を儲けた。ウニボールのレイアのメソッド EnterBall では、この入力値を使用して GetNextFrame を呼び出している。 プレイヤーの好みの速度でウニが動く。反射神経の高いプレイヤーへの配慮だ。ウニが枠外に飛び出すと、ウニを避けたと言う事で得点を加算する。そして、枠内のランダムな位置にワープさせる。 主人公の位置とウニの位置が同じ、つまりウニに当たったら、ゲーム・オーバーとなる。枠内のランダムな位置の設定方法を工夫すると、面白みが増すだろう。ぜひ挑戦して頂きたい。
6 二次元空間の中の三次元世界へ
画面は二次元である。この二次元の空間に立体的に見えるように何かを表示する。つまり人間の目を欺くのが、いわゆる3Dグラフィックスである。算数脳の私でも、ここまでは理解できる。
二次元なら算数脳の私でも何とかなる。ところが三次元になった途端に、頭から煙がでるような数式が並ぶ。そこで Ricardo Cabello さんが作成した Three.js を使わせて頂いて、頭の煙を最小に
抑える事にする。このライブラリを使用して、ウニボールの3D版に挑戦する。
ウニボールの2D版では地べたしか無かった。そして地べたを囲む枠があった。この枠を3Dにすると壁になる。しかも左右の壁と奥側と手前側の4面の壁だ。加えて地べたと天井の2面が加わる。 一つ次元が加わるだけで、6面になるのだ。まずは、この6面から描く事にしよう。
面を描く前に、3D上の座標系について話しておく。ネットで3DCGを検索すると、ローカル座標とかワールド座標などが出てくる。このような難しい座標の話は、私の手に余る。Three.js が 難しい概念部分は吸収してくれる。算数脳で押えておく座標系とは、原点はどこかである。2Dの場合は描画領域の四角形の左上が原点である。当ゲームエンジンの3Dの場合は、 描画領域の四角形の中心点を原点とする。描画領域の四角形のサイズが 100×100 なら中心点は(x = 50, y = 50) である。この点を原点(0, 0, 0) として、左右、上下、前後の位置を表現する。 左右はX軸、上下はY軸、前後はZ軸だ。2DでのY軸の正の方向は下向きだった。3Dでは正の方向は上、負の方向は下となる。つまり数学と同様の空間の扱いになる。
Z軸の正負の向きはどうか?これは使用する3Dのライブラリに依存する。OpenGL 系では奥側が負、手前側が正である。Three.js は OpenGL 系に従っている。Microsoft の DirectX は 逆を採用している。ところでZ軸の z = 0 とはどこだろう。ここからは奥側、ここからは手前側とするものは、何なのか?それは、当ゲームエンジンが呼び出す THREE.PerspectiveCamera の引数で 決定する。見える範囲を、手前側の値と奥側の値として与える。手前側の値が z = 0 となる。 3D対応版のゲームエンジンのソースをあげておく。
ウニボールの2D版では地べたしか無かった。そして地べたを囲む枠があった。この枠を3Dにすると壁になる。しかも左右の壁と奥側と手前側の4面の壁だ。加えて地べたと天井の2面が加わる。 一つ次元が加わるだけで、6面になるのだ。まずは、この6面から描く事にしよう。
面を描く前に、3D上の座標系について話しておく。ネットで3DCGを検索すると、ローカル座標とかワールド座標などが出てくる。このような難しい座標の話は、私の手に余る。Three.js が 難しい概念部分は吸収してくれる。算数脳で押えておく座標系とは、原点はどこかである。2Dの場合は描画領域の四角形の左上が原点である。当ゲームエンジンの3Dの場合は、 描画領域の四角形の中心点を原点とする。描画領域の四角形のサイズが 100×100 なら中心点は(x = 50, y = 50) である。この点を原点(0, 0, 0) として、左右、上下、前後の位置を表現する。 左右はX軸、上下はY軸、前後はZ軸だ。2DでのY軸の正の方向は下向きだった。3Dでは正の方向は上、負の方向は下となる。つまり数学と同様の空間の扱いになる。
Z軸の正負の向きはどうか?これは使用する3Dのライブラリに依存する。OpenGL 系では奥側が負、手前側が正である。Three.js は OpenGL 系に従っている。Microsoft の DirectX は 逆を採用している。ところでZ軸の z = 0 とはどこだろう。ここからは奥側、ここからは手前側とするものは、何なのか?それは、当ゲームエンジンが呼び出す THREE.PerspectiveCamera の引数で 決定する。見える範囲を、手前側の値と奥側の値として与える。手前側の値が z = 0 となる。 3D対応版のゲームエンジンのソースをあげておく。
7 奥側の壁を作る
6面の中の一つである奥側の壁を作ろう。描くでは無く作るのだ。描くのは three.js の Renderer が行う。描くと言う作業は、頭から煙がでるような数式を駆使しなければならない。それを
Renderer が行ってくれる。この Renderer には数種類あるのだが、当ゲームエンジンでは、THREE.CanvasRenderer を採用している。これは GPU を使用せずに、CPU のみで描画をエミュレートする。
当然 GPU を使用しないので、GPU を使用する Renderer より低速である。しかし GPU を搭載していない機器でも動かす事ができる。


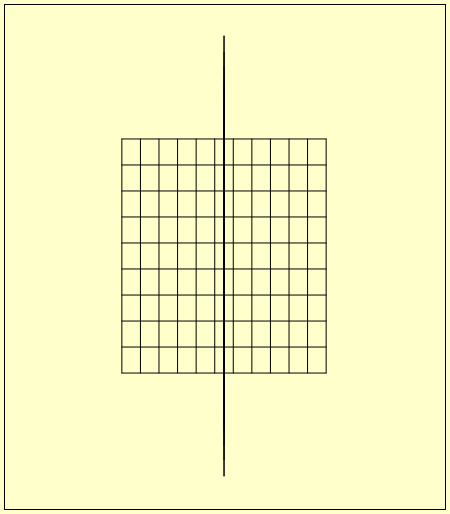
さて、作るに話を戻そう。壁を作りたいので、壁と言う物(オブジェクト)を作る。この壁には水平線と垂直線が描かれるとする。すると、水平線と垂直線のオブジェクトが必要になる。 まず水平線と言う物を考えてみよう。線を描くには2点が必要だ。この点は何にするか?ここは、単純に描画領域の左端から右端までとする。壁は地面に垂直に立たせる。Z軸は z = 0 とする。この条件なら後は x と y の座標で考えれば良い。y の値は描画領域の上端から下端までとする。
このようにして、作成したのが左側の図である。描画領域の左端から右端になっていないと思うかも知れない。「見える範囲を、手前側の値と奥側の値として与える。手前側の値が z = 0 となる」 を思い出して欲しい。当ゲームエンジンでは手前側の値には1を設定している。Renderer が手前側の値を三次元空間内の z = 0 の位置として計算し描画する。
それでは、手前側の値をゼロにしたら良いかと言えば、そうでもない。そこは貴方がいる世界になり、二次元の空間に立体的に見えるようにする世界から飛び出した世界になる。 貴方は画面に触れる事ができるでしょう?触れる事ができると言う事は、画面の面は仮想世界でなく、貴方がいる現実世界なのだ。描きたい物は、少し奥側に移動すると思った方が良い。 数学的には画面を飛び出す事は可能だ。だから計算はできる。しかし計算ができる事と、人間に見えるか見えないかは別物である。これ以上は私の説明能力限界を越えるので、止めておく。 ここは、算数脳でも3Dができる事を楽しむ場所とする。
下記のコードは、左側の図のようになるコードである。このままでは、奥側の壁にならない。そこで、GridBackWall.position.z = -sz.cx; として壁を奥に移動する。 移動したイメージが右側の図である。ここまでを纏めると 1) Renderer に描いて欲しい物を作成する。2) 作成した物は移動する事ができる。となる。


さて、作るに話を戻そう。壁を作りたいので、壁と言う物(オブジェクト)を作る。この壁には水平線と垂直線が描かれるとする。すると、水平線と垂直線のオブジェクトが必要になる。 まず水平線と言う物を考えてみよう。線を描くには2点が必要だ。この点は何にするか?ここは、単純に描画領域の左端から右端までとする。壁は地面に垂直に立たせる。Z軸は z = 0 とする。この条件なら後は x と y の座標で考えれば良い。y の値は描画領域の上端から下端までとする。
このようにして、作成したのが左側の図である。描画領域の左端から右端になっていないと思うかも知れない。「見える範囲を、手前側の値と奥側の値として与える。手前側の値が z = 0 となる」 を思い出して欲しい。当ゲームエンジンでは手前側の値には1を設定している。Renderer が手前側の値を三次元空間内の z = 0 の位置として計算し描画する。
それでは、手前側の値をゼロにしたら良いかと言えば、そうでもない。そこは貴方がいる世界になり、二次元の空間に立体的に見えるようにする世界から飛び出した世界になる。 貴方は画面に触れる事ができるでしょう?触れる事ができると言う事は、画面の面は仮想世界でなく、貴方がいる現実世界なのだ。描きたい物は、少し奥側に移動すると思った方が良い。 数学的には画面を飛び出す事は可能だ。だから計算はできる。しかし計算ができる事と、人間に見えるか見えないかは別物である。これ以上は私の説明能力限界を越えるので、止めておく。 ここは、算数脳でも3Dができる事を楽しむ場所とする。
下記のコードは、左側の図のようになるコードである。このままでは、奥側の壁にならない。そこで、GridBackWall.position.z = -sz.cx; として壁を奥に移動する。 移動したイメージが右側の図である。ここまでを纏めると 1) Renderer に描いて欲しい物を作成する。2) 作成した物は移動する事ができる。となる。
// レイアのサイズを得る var sz = this.GameUtl.GetSize(); // 壁と言う物(オブジェクト)を作る var GridBackWall = new THREE.Object3D(); // 材質を作る var Material = new THREE.LineBasicMaterial({ color: "black" }); // 横線 for (var sy = -(sz.cy / 2); sy <= (sz.cy / 2); sy += this.ExpCy) { var v1 = new THREE.Vector3(-(sz.cx / 2), sy, 0); var v2 = new THREE.Vector3((sz.cx / 2), sy, 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridBackWall.add(new THREE.Line(geo, Material)); } // 縦線 for (var sx = -(sz.cx / 2); sx <= (sz.cx / 2); sx += this.ExpCx) { var v1 = new THREE.Vector3(sx, -(sz.cy / 2), 0); var v2 = new THREE.Vector3(sx, (sz.cy / 2), 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridBackWall.add(new THREE.Line(geo, Material)); } // グリッドオブジェクト生成 p.Grid = new THREE.Object3D(); // 壁をグリッドオブジェクトに追加 p.Grid.add(GridBackWall); // グリッドオブジェクトをシーンに追加 this.GameUtl.Core.Scene.add(p.Grid);
8 左右の壁を作る
今度は、左右の壁を作る。まず左側の壁から取りかかる。左の壁も地面に垂直にする。幅も高さも奥側の壁と同様だ。奥側の壁は x と y の座標で考えた。左側の壁で固定なのは x である。
よって x の代わりに z で考える。
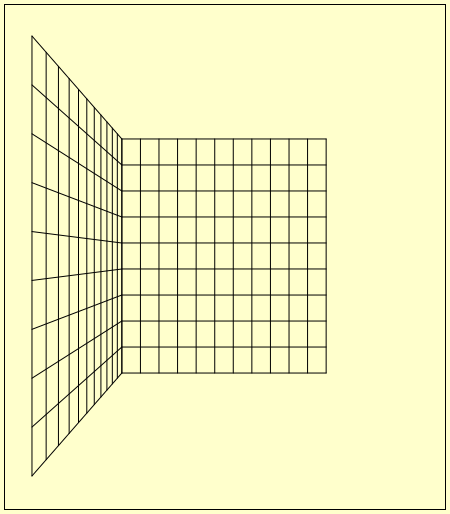
 1番目の図は、奥側の壁を作った時と同様に、水平線と垂直線を作り、それらの物を壁の部品として壁に加えたものである。
1番目の図は、奥側の壁を作った時と同様に、水平線と垂直線を作り、それらの物を壁の部品として壁に加えたものである。
1) var GridLeftWall = new THREE.Object3D(); で壁を作る。
2) THREE.Vector3 で点を指定する。
3) THREE.Line で線を作る。
4) GridLeftWall.add で壁の部品とする。
5) this.GameUtl.Core.Scene.add で壁を追加する。
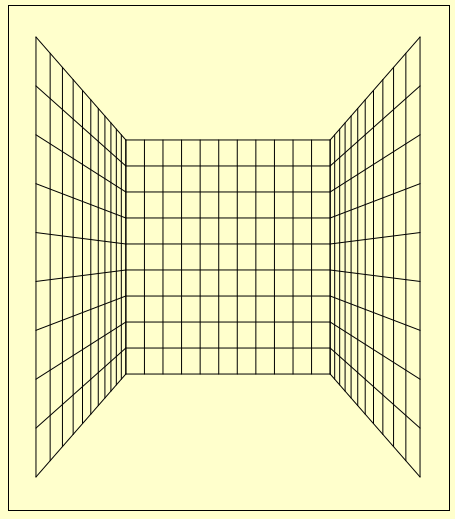
上記の処理で描画領域の中央に垂直線が表示された。左側の壁は、まだ描画領域の左右中央にあり、壁を真横から見ている状態である。 この状態に、GridLeftWall.position.x = -(sz.cx / 2); として左に移動したのが、2番目の図である。
拝むように手を立てて、親指が鼻にあたるようにする。左手なら左側に、右手なら右側に真っ直ぐに動かす。耳の位置あたりまで動かすと、手のひらが視界にあるのがわかる。 感覚的に同様の事が、二次元の空間に立体的に見えるようにする世界で行われると考えれば良い。
右側の壁の作成は左側の壁と同様である。GridRightWall.position.x = (sz.cx / 2); として、右側へ移動する。ここまでの様子が3番目の図だ。


 1番目の図は、奥側の壁を作った時と同様に、水平線と垂直線を作り、それらの物を壁の部品として壁に加えたものである。
1番目の図は、奥側の壁を作った時と同様に、水平線と垂直線を作り、それらの物を壁の部品として壁に加えたものである。1) var GridLeftWall = new THREE.Object3D(); で壁を作る。
2) THREE.Vector3 で点を指定する。
3) THREE.Line で線を作る。
4) GridLeftWall.add で壁の部品とする。
5) this.GameUtl.Core.Scene.add で壁を追加する。
上記の処理で描画領域の中央に垂直線が表示された。左側の壁は、まだ描画領域の左右中央にあり、壁を真横から見ている状態である。 この状態に、GridLeftWall.position.x = -(sz.cx / 2); として左に移動したのが、2番目の図である。
拝むように手を立てて、親指が鼻にあたるようにする。左手なら左側に、右手なら右側に真っ直ぐに動かす。耳の位置あたりまで動かすと、手のひらが視界にあるのがわかる。 感覚的に同様の事が、二次元の空間に立体的に見えるようにする世界で行われると考えれば良い。
右側の壁の作成は左側の壁と同様である。GridRightWall.position.x = (sz.cx / 2); として、右側へ移動する。ここまでの様子が3番目の図だ。
9 床を作る
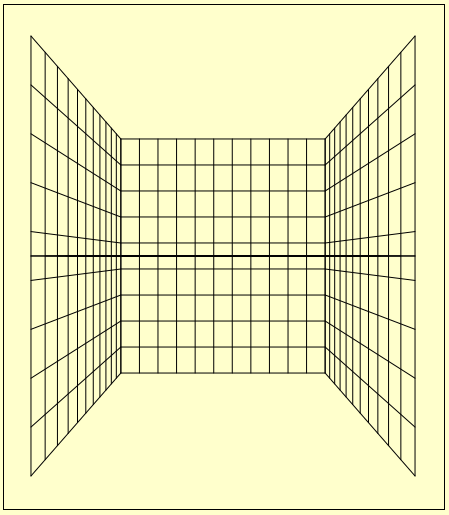
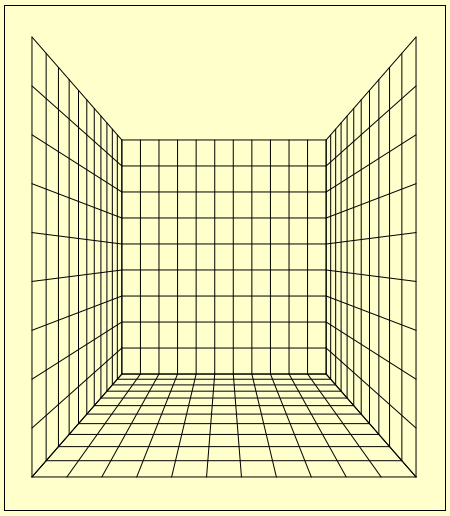 今度は床を作る。床で固定なのは y である。よって x と z で考える。床には高さは無い。よって sz.cy は使用しない。水平線も垂直線もグリッドで分割する幅と高さは、this.ExpCx
となる。床を作っただけの状態が左図である。これを GridFloor.position.y = -(sz.cy / 2); として移動する。移動後のものが右図である。
今度は床を作る。床で固定なのは y である。よって x と z で考える。床には高さは無い。よって sz.cy は使用しない。水平線も垂直線もグリッドで分割する幅と高さは、this.ExpCx
となる。床を作っただけの状態が左図である。これを GridFloor.position.y = -(sz.cy / 2); として移動する。移動後のものが右図である。さて、後は天井と手前の壁が残った。この二つについては描画をしない。描画すると、鳥籠のような状態になる。ウニボールを避ける動作を、プレイヤーが主人公を動かして行うわけだが、 プレイヤーから見ると鳥籠はうざったい。私としては、必要ないと判断した。描画はしないが、後でウニボールをバウンドさせるために、位置や大きさは必要だ。 これについては、後にバウンドの為のデータの保持で説明する。
奥側の壁と左右の壁と床を作るコードが下記になる。
// 面とグリッド生成 clsSample3D.prototype.SetGrid = function(p) { // レイアのサイズを得る var sz = this.GameUtl.GetSize(); // 壁と床オブジェクト生成 var GridBackWall = new THREE.Object3D(); var GridLeftWall = new THREE.Object3D(); var GridRightWall = new THREE.Object3D(); var GridFloor = new THREE.Object3D(); // 罫線質感生成 var Material = new THREE.LineBasicMaterial({ color: "black" }); // 奥側と左右の壁の横線 for (var sy = -(sz.cy / 2); sy <= (sz.cy / 2); sy += this.ExpCy) { // 奥側の壁 var v1 = new THREE.Vector3(-(sz.cx / 2), sy, 0); var v2 = new THREE.Vector3((sz.cx / 2), sy, 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridBackWall.add(new THREE.Line(geo, Material)); // 左右の壁 var v1 = new THREE.Vector3(0, sy, -sz.cx); var v2 = new THREE.Vector3(0, sy, 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridLeftWall.add(new THREE.Line(geo, Material)); GridRightWall.add(new THREE.Line(geo, Material)); } // 奥側と左右の壁と床 for (var sx = -(sz.cx / 2); sx <= (sz.cx / 2); sx += this.ExpCx) { // 奥側の壁の縦線 var v1 = new THREE.Vector3(sx, -(sz.cy / 2), 0); var v2 = new THREE.Vector3(sx, (sz.cy / 2), 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridBackWall.add(new THREE.Line(geo, Material)); // 左右の壁の縦線 var v1 = new THREE.Vector3(0, -(sz.cy / 2), sx - (sz.cx / 2)); var v2 = new THREE.Vector3(0, (sz.cy / 2), sx - (sz.cx / 2)); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridLeftWall.add(new THREE.Line(geo, Material)); GridRightWall.add(new THREE.Line(geo, Material)); // 床の横線 var v1 = new THREE.Vector3(-(sz.cx / 2), 0, sx - (sz.cx / 2)); var v2 = new THREE.Vector3((sz.cx / 2), 0, sx - (sz.cx / 2)); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridFloor.add(new THREE.Line(geo, Material)); // 床の縦線 var v1 = new THREE.Vector3(sx, 0, -sz.cx); var v2 = new THREE.Vector3(sx, 0, 0); var geo = new THREE.Geometry(); geo.vertices.push(v1, v2); GridFloor.add(new THREE.Line(geo, Material)); } // 壁と床の位置に移動 GridBackWall.position.z = -sz.cx; GridLeftWall.position.x = -(sz.cx / 2); GridRightWall.position.x = (sz.cx / 2); GridFloor.position.y = -(sz.cy / 2); // グリッドオブジェクト生成 p.Grid = new THREE.Object3D(); // 壁と床をグリッドオブジェクトに追加 p.Grid.add(GridBackWall); p.Grid.add(GridLeftWall); p.Grid.add(GridRightWall); p.Grid.add(GridFloor); // グリッドオブジェクトをシーンに追加 this.GameUtl.Core.Scene.add(p.Grid); }
10 主人公を生成する
「子作り」と言う表現があるのだから、主人公を作るでも良かったのだが、ちょっと抵抗を覚えた(^^) まぁ作る事に変わりはないのだが、主人公だし良しとしよう。
主人公の生成には、canvas を使用する。以下にコードを示す。
2) THREE.Texture で 1) の canvas を指定する。
3) THREE.MeshBasicMaterial で材質に 2) の結果を指定する。
4) THREE.PlaneGeometry で形状を生成する。
5) THREE.Mesh に形状と材質を指定して描画する物を生成する
6) 描画する物を移動してシーンに追加する。
上記の処理を終えた時点では、主人公は描画されない。正確には、黒の完全透明な絵が描画される。材質として与えた canvas に描かれたものが描画されるのだ。 この canvas に、コマ送りのタイミングで主人公のドット絵を描画し、足踏みを表現する。
// 主人公生成 clsSample3D.prototype.SetHero = function(p) { // レイアのサイズを得る var sz = this.GameUtl.GetSize(); // 主人公を描画する Canvas を生成 var HeroCanvas = this.GameUtl.NewHiddenCanvas(g_idStage, this.ExpCx, this.ExpCy); // 生成した Canvas をテクスチャとする var HeroTexture = new THREE.Texture(HeroCanvas); // 画像を指定したmaterialの用意 var HeroMaterial = new THREE.MeshBasicMaterial({ map:HeroTexture }); // 主人公の形状を生成 var HeroGeometry = new THREE.PlaneGeometry(this.ExpCx * 2, this.ExpCy * 2); // メッシュを生成 p.HeroMesh = new THREE.Mesh(HeroGeometry, HeroMaterial); // 床に移動する p.HeroMesh.position.y = -(sz.cy / 2) + this.ExpCy - 4; p.HeroMesh.position.z = -(sz.cx / 2); // 主人公をシーンに追加 this.GameUtl.Core.Scene.add(p.HeroMesh); // コンテキストを生成 p.HeroCtx = HeroCanvas.getContext("2d"); }1) this.GameUtl.NewHiddenCanvas で非表示の canvas を生成する。
2) THREE.Texture で 1) の canvas を指定する。
3) THREE.MeshBasicMaterial で材質に 2) の結果を指定する。
4) THREE.PlaneGeometry で形状を生成する。
5) THREE.Mesh に形状と材質を指定して描画する物を生成する
6) 描画する物を移動してシーンに追加する。
上記の処理を終えた時点では、主人公は描画されない。正確には、黒の完全透明な絵が描画される。材質として与えた canvas に描かれたものが描画されるのだ。 この canvas に、コマ送りのタイミングで主人公のドット絵を描画し、足踏みを表現する。
11 ウニボールを作る
ウニボールは球体として作る。球体は THREE.SphereGeometry で作成する。three.js は基本的な形状を生成するメソッドを提供している。球体と言っても完全な球体ではない。
これは円でも同様である。六角形より八角形、八角形より十角形、十角形より十二角形と頂点の数が増えていくにつれ、円のように見えてくる。頂点の数を分割数として呼び出す。
THREE.SphereGeometry(半径, 経度分割数, 緯度分割数); となるのだが、この分割数が多い程に計算量は増える。球体のように見える程度の分割数が良いだろう。
これで、登場する物は揃ったので、実際に動くものとソースをあげて、以降の節は話を進めていく事にする。 3D版ウニボールで動きを確認して欲しい。 それと3D版ウニボールのソースをあげておく。
ウニボールの生成は clsSample3D.prototype.SetBall で行っている。「後にバウンドの為のデータの保持」として説明を保留してしていた部分は、clsSample3D のコンストラクタの中の、 「反射処理の為に壁の位置を記憶する」の箇所で、6面の大きさを this.Wall に記憶している。壁と床と天井は動かないので、初期データとして保持する。 データの中身は面の頂点を、a, b, c, d としている。それぞれの値の意味は clsSample3D.prototype.SetGrid を見ればわかると思う。
これで、登場する物は揃ったので、実際に動くものとソースをあげて、以降の節は話を進めていく事にする。 3D版ウニボールで動きを確認して欲しい。 それと3D版ウニボールのソースをあげておく。
ウニボールの生成は clsSample3D.prototype.SetBall で行っている。「後にバウンドの為のデータの保持」として説明を保留してしていた部分は、clsSample3D のコンストラクタの中の、 「反射処理の為に壁の位置を記憶する」の箇所で、6面の大きさを this.Wall に記憶している。壁と床と天井は動かないので、初期データとして保持する。 データの中身は面の頂点を、a, b, c, d としている。それぞれの値の意味は clsSample3D.prototype.SetGrid を見ればわかると思う。
12 ウニボールが狙うもの
ウニボールが狙うものは主人公である。だが天井から直線的に主人公を狙うと、プレイヤーが避けやすくなる。かと言って壁にバウンドさせて、主人公を狙うような数学的必殺技のコードは、
私には書けない(__!) そこで、2回に1回の確率で主人公を直線的に狙い、2回に1回の確率で主人公の周辺を狙う事にする。周辺は主人公のいる場所から前後に -5 ~ +5 を乱数で取得し、
さらに左右も -5 ~ +5 を乱数で取得する。巧くいけば主人公が逃げる方向で当たるだろう。ウニの味方をしているわけではないよ(__!)
ウニは、天井の位置から狙いを定めた位置までを直線的に移動する。どのように直線を割り出すか?ここで登場するのがベクトルである。 私の数学脳への道を閉ざした、数学の授業が嫌いになったベクトルだ。これに行列でも出てこようものなら、悪夢の日々が蘇るのだ。

しかし、3Dゲームを作るには、ベクトルが必須となる。 日頃、お世話になっているサイト ゲームプログラミング技術集 をあげておく。 THREE.Vector3 で生成する点はベクトルである。点だけでは方向が無いのでベクトルにはならない。暗黙的に座標軸との交点(ベクトルの開始点)は原点となる。
ウニボールの現在の位置をA点、ウニボールが狙う位置をB点とする。A点からB点へ向かう方向ベクトルは、B - A となる。A点からB点へ向かう方向が東なら東の情報を持つ。 決して、A点とB点を結ぶわけではない。B - A = A点からB点へ向かう方向が同じで且つ距離も同じで出発点は原点とするベクトル となる。ここは、私と同じ算数脳の方の為にじっくりと進む。 決して、A点とB点を結ぶわけではない。重要なので二度言いました。
このA点からB点へ向かう方向ベクトルの単位ベクトルを求めて、ウニボールの直径を掛けると移動量(距離)となる。さらに、A を足すと移動先となる。
var A = new THREE.Vector3(ウニボールの現在の位置の座標);
var B = new THREE.Vector3(ウニボールが狙う位置の座標);
var P1 = B.sub(A);
var P2 = P1.normalize();
var P3 = P2.multiplyScalar(ウニボールの直径).add(A);
これが、1コマで描くウニボールの位置となり、移動後の現在位置となる。なお図の中の単位円は解り易くする為に大きく描いてある。
ウニは、天井の位置から狙いを定めた位置までを直線的に移動する。どのように直線を割り出すか?ここで登場するのがベクトルである。 私の数学脳への道を閉ざした、数学の授業が嫌いになったベクトルだ。これに行列でも出てこようものなら、悪夢の日々が蘇るのだ。

しかし、3Dゲームを作るには、ベクトルが必須となる。 日頃、お世話になっているサイト ゲームプログラミング技術集 をあげておく。 THREE.Vector3 で生成する点はベクトルである。点だけでは方向が無いのでベクトルにはならない。暗黙的に座標軸との交点(ベクトルの開始点)は原点となる。
ウニボールの現在の位置をA点、ウニボールが狙う位置をB点とする。A点からB点へ向かう方向ベクトルは、B - A となる。A点からB点へ向かう方向が東なら東の情報を持つ。 決して、A点とB点を結ぶわけではない。B - A = A点からB点へ向かう方向が同じで且つ距離も同じで出発点は原点とするベクトル となる。ここは、私と同じ算数脳の方の為にじっくりと進む。 決して、A点とB点を結ぶわけではない。重要なので二度言いました。
このA点からB点へ向かう方向ベクトルの単位ベクトルを求めて、ウニボールの直径を掛けると移動量(距離)となる。さらに、A を足すと移動先となる。
var A = new THREE.Vector3(ウニボールの現在の位置の座標);
var B = new THREE.Vector3(ウニボールが狙う位置の座標);
var P1 = B.sub(A);
var P2 = P1.normalize();
var P3 = P2.multiplyScalar(ウニボールの直径).add(A);
これが、1コマで描くウニボールの位置となり、移動後の現在位置となる。なお図の中の単位円は解り易くする為に大きく描いてある。
13 ウニボールの跳ね返り
 ウニボールが面に当たると、ウニボールは跳ね返る。これを実装する為には、どの面に当たったかを判定する必要がある。
これは、平面と線分の交点を求める方法 を参考にさせて頂いた。
参考サイトによると「平面方程式から平面上の点Pと法線Nが分かる」とある。これが、私には理解ができない(__!)
ウニボールが面に当たると、ウニボールは跳ね返る。これを実装する為には、どの面に当たったかを判定する必要がある。
これは、平面と線分の交点を求める方法 を参考にさせて頂いた。
参考サイトによると「平面方程式から平面上の点Pと法線Nが分かる」とある。これが、私には理解ができない(__!) 参考サイトでは、平面上の点P = Vertex3D( PL.a * PL.d, PL.b * PL.d, PL.c * PL.d ); として求めている。そのまま、真似をしたら求まるだろう。しかし、イメージできないものを真似しても、 自分自身の腑に落ちない。
参考サイトの図を見ると、平面上の点Pとは、どうやら面の中心点のようである。ならば、4頂点の和÷4で中心点を求める事にする。左図は面の頂点(a,b,c,d) に対する頂点の和を、 青色のベクトルで示してある。これを4で割ると言う事は4分の1に縮小する事になる。この方法は正確には重心点を求める簡易な方法である。 だから必ずしも重心点が中心点となるとは、限らない。だが、長方形なら成り立つ。
var P = (Plane.a.clone().add(Plane.b).add(Plane.c).add(Plane.d)).divideScalar(4); として平面上の点Pを求めた。
次に必要なのは、法線だ。これは点Pを通る面に直交する単位ベクトルである。これを求めるには外積を用いる。なぜ外積で法線が求まるのかは、私には説明できない。説明すると言う事は、 証明する事に他ならない。算数脳の私には無理である。これは自明として受け入れよう。下左側の枠に法線の求め方を掲載した。
法線を求める
// 面の中心点と線分始点のベクトル(Pからvaに向かう) var pa = va.clone().sub(P); // 面の中心点と線分終点のベクトル(Pからvbに向かう) var pb = vb.clone().sub(P); // 面に対して垂直なベクトル=法線ベクトル var ab = Plane.b.clone().sub(Plane.a); var ad = Plane.d.clone().sub(Plane.a); var N = ab.cross(ad).normalize();
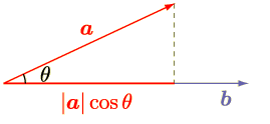 平面上の点Pと法線が求められたので、後は参考サイトに従って、交差判定と交点を求める。「PAベクトル、PBベクトルをそれぞれNと内積」とある。内積とは、2つのベクトルにおいて、
一方のベクトルを他方のベクトルに投影した時の、成分である。右図は、ベクトル a をベクトル b に投影した時の成分を表している。
平面上の点Pと法線が求められたので、後は参考サイトに従って、交差判定と交点を求める。「PAベクトル、PBベクトルをそれぞれNと内積」とある。内積とは、2つのベクトルにおいて、
一方のベクトルを他方のベクトルに投影した時の、成分である。右図は、ベクトル a をベクトル b に投影した時の成分を表している。pa pb それぞれの平面法線との内積は、
var dot_PA = pa.clone().dot(N); var dot_PB = pb.clone().dot(N); となる。参考サイトでは、線端が平面上にあった時の計算の誤差を考慮している。しかし、当方は無視する事にする。 clsSample3D.prototype.IntersectPlaneAndLine は、上記の計算を行っている。交差した場合は交差点と法線を返す。
反射ベクトルは、ずばり、反射ベクトルを求める を参考にさせて頂いた。 Rは反射ベクトル、Fは進行ベクトル、Nは法線ベクトルとする。R = F + 2(-F・N)N となる。この計算は clsSample3D.prototype.DoReflection で行っている。
これで、ウニボールが箱の中を飛び跳ねる事ができた。
14 主人公を描画する
clsSample3D.prototype.SetHero で主人公を生成した。主人公の形状は板(Plane) である。そして材質に非表示の canvas を与えた。ここでは、非表示の canvas に主人公を描画する。
これは、2Dで行った事とほとんど変わらない。主人公の向きと現在のフレーム番号から、ドット絵の転送元の位置を計算する。後は、非表示の canvas に drawImage で描画する。
描画を終えたら、p.HeroMesh.material.map.needsUpdate = true; として材質の変更があった事を知らせる為に、フラグを立てる。そうすると、二次元の空間に立体的に見えるように
Renderer が巧く描いてくれる。主人公の描画は、clsSample3D.prototype.DrawHero で行っている。さらに、主人公とボールの衝突判定も行っている。
四角形と球体の衝突判定を行うわけだが、面倒臭い(__!)
衝突判定で、最も簡単な形状の組み合わせは円だ。球体は円と置き換える事もできる。双方の距離が双方の半径の和より小さいなら衝突している。主人公も円とみなして、判定を行う。 それでは、主人公の半径をいくらにするかだ。主人公チップの高さは56である。上の透過部分を除くと幅との差はあまりない。そこで幅の半分から適当に透過部分を減算して、主人公の 半径とする。人間の目を欺ける程度に調整したら良い。
衝突判定で、最も簡単な形状の組み合わせは円だ。球体は円と置き換える事もできる。双方の距離が双方の半径の和より小さいなら衝突している。主人公も円とみなして、判定を行う。 それでは、主人公の半径をいくらにするかだ。主人公チップの高さは56である。上の透過部分を除くと幅との差はあまりない。そこで幅の半分から適当に透過部分を減算して、主人公の 半径とする。人間の目を欺ける程度に調整したら良い。
15 キー入力とコマの同期
2Dの時は、window.addEventListener('keydown', this.KeyDown.bind(this)); として、キー入力イベントの設定を行っていた。キー入力とコマを描く処理は同期するか?javascript は、
シングル・スレッドだから、同期するだろうと思われるかも知れない。requestAnimationFrame は一定時間に達したら実行する。キー入力は、
割り込みが
発生したら実行する。両者を同期させる者は、何処にもいない。故に同期はしないとなる。マウス入力も同様に同期はしない。
プレイヤーは画面を見ながら操作を行う。主人公を右へ動かす操作を行ったとしよう。右へ動かすキー入力により、イベントが発生し主人公の位置を変更する。位置を変更するタイミングと フレーム番号が変わるタイミングは、一致しない。これは、プレイヤーに違和感を与えるだろう。そこで、当ゲームエンジンでは、clsGameUtl.prototype.EnterKeyDown を設けて、 ゲームループの中で、キー入力イベントを処理する関数を、コールバックする事にする。
ゲーム実装クラスの clsSample3D.prototype.Run において、this.GameUtl.EnterKeyDown(this.KeyDown); を呼び出している。 ゲームエンジンは、キー入力があった場合はバッファに記憶するだけにする。ゲームループの中で、記憶したキー入力があれば指定された関数をコールバックする。
clsSample3D.prototype.DrawHero では、主人公の位置を取得して、位置の変更を行っている。向きの変更はコマの処理で行っている。下記の部分だ。
プレイヤーは画面を見ながら操作を行う。主人公を右へ動かす操作を行ったとしよう。右へ動かすキー入力により、イベントが発生し主人公の位置を変更する。位置を変更するタイミングと フレーム番号が変わるタイミングは、一致しない。これは、プレイヤーに違和感を与えるだろう。そこで、当ゲームエンジンでは、clsGameUtl.prototype.EnterKeyDown を設けて、 ゲームループの中で、キー入力イベントを処理する関数を、コールバックする事にする。
ゲーム実装クラスの clsSample3D.prototype.Run において、this.GameUtl.EnterKeyDown(this.KeyDown); を呼び出している。 ゲームエンジンは、キー入力があった場合はバッファに記憶するだけにする。ゲームループの中で、記憶したキー入力があれば指定された関数をコールバックする。
clsSample3D.prototype.DrawHero では、主人公の位置を取得して、位置の変更を行っている。向きの変更はコマの処理で行っている。下記の部分だ。
// 主人公の位置を取得
var pos = this.GetHeroPosition();
// 位置を設定
p.HeroMesh.position.x = pos.dx;
p.HeroMesh.position.z = pos.dz;
// fps からフレーム番号を得る
var frame = this.GameUtl.GetNextFrame(p, 256, this.ExpFrameNum);
// 描画するコマが変化したなら...
if (p.Frame != frame || this.GameOver) {
// コマの処理
}
厳密に同期をとるなら、向きの変更があった場合も、コマの処理をするべきである。しかし、その様な厳密さは不要と判断したので、向きの変更には対処していない。